Sjednocení, průnik a doplněk pravděpodobnosti
Aditivní množinové funkce
Ze střední školy by si každý měl pamatovat definici reálné funkce:
Je dána množina S. Funkce f je množina uspořádaných dvojic (s,r), kde s je prvek S a r je reálné číslo, přitom každý prvek z množiny S se vyskytuje právě jednou.
Tato definice zní trochu formálně, ale musíme si uvědomit, že zajišťuje intuitivně chápaný pojem přiřazení či zobrazení. Tedy ke každému prvku z S jako vzoru existuje nějaké reálné číslo jako jeho obraz. Žádný prvek z S se neopakuje, takže je vyloučeno, aby se zobrazil jako dvě reálná čísla. Takto chápaná funkce se nazývá bodová funkce.
Často je třeba uvažovat i tak, že čísla přiřazujeme podmnožinám základní množiny S. Jedná se jistě také o funkce, ale mají tu zvláštnost, že definičním oborem je systém podmnožin základní množiny, nikoliv základní množina. Zobrazují podmnožiny zakladní množiny, nikoliv prvky základní množiny.
Snad nejjednodušší množinovou funkcí je počet prvků množiny, případně počet prvků s určitou vlastností. Počet prvků může být i nekonečný a pak má spíš smysl hovořit o objemu, ploše či délce. To jsou jen příklady množinových funkcí, se kterými jsme měli možnost se setkat při studiu klasické nebo geometrické definice pravděpodobnosti.
Nejžádanější vlastnost množinové funkce je aditivnost. Je dána základní množina S.
Dvě množiny `A \subset S a B\subset S` nazýváme DISJUNKTNÍ, jestliže nemají společný prvek.
Množinová funkce m se nazývá ADITIVNÍ, jestliže pro libovolné dvě disjunktní množiny A a B platí m(A `\cup` B) = m(A) + m(B).
Jak již jsme se zmínili, má tuto vlastnost objem, plocha, délka a hmotnost. Hustota je bodová funkce. Teplota je bodová funkce, teplo je množinová funkce, protože se tepla dvou disjunktních těles sčítají.
Okamžitou rychlost jako funkci času považujeme za bodovou funkci. Průměrná rychlost je množinová funkce, ale není aditivní, neboť průměrnou rychlost za nějaký časový úsek nedostaneme jako součet průměrných rychlostí za podúseky. Překonanou vzdálenost považujeme za aditivní množinovou funkci, protože vzdálenost překonanou za nějaký časový úsek získáme jako součet vzdáleností za podúseky.
Po pravděpodobnosti žádáme, aby to byla množinová funkce aditivní, nezáporná a pravděpodobnost základní množiny S aby byla jedna.
Pro práci s množinami se děti ve škole učí používat Vennovy diagramy. Na nich je dobře vidět, jak se tvoří průnik či sjednocení, co je doplněk a další operace s množinami. Děti si nemusí pamatovat vzorečky, protože je vidí na diagramech. K tomu chceme dospět i v počtu pravděpodobnosti. Musíme si uvědomit, že pravděpodobnost je nezáporná aditivní množinová funkce a že má, kromě omezenosti jedničkou, stejné vlastnosti jako plocha. Musí tedy platit, že to, co platí pro plochy, platí i pro pravděpodobnosti. Když si k tomu ještě navíc představíme, že plocha základního obrazce je jedna, je analogie úplná.
Výsledkem tohoto výkladu je nakonec jen to, že si základní vzorečky v počtu pravděpodobnosti můžeme odvozovat pomocí Vennových diagramů a budou platit.
Počet pravděpodobnosti a teorie množin (nepovinné)
Počet pravděpodobnosti a pravidla pro zacházení s jevy mají souvislost s teorií množin do takové míry, že je možné pro zajímavost předložit seznam pojmů z počtu pravděpodobnosti a k ním ekvivalentní pojmy z teorie množin.
- jev - podmnožina
- pravděpodobnost - aditivní množinová funkce
- neslučitelné jevy - disjunktní podmnožiny
- průnik jevu - průnik podmnožin
A a B - A ∩ B
Sjednocení jevu - sjednocení podmnožin
A nebo B - A `\cup` B
- jev jistý - základní množina
- jev nemožný - prázdná množina
- A je následek B - B je podmnožinou A
Když někdo řekne prázdný jev místo nemožný, není to chyba a všichni vědí, o co jde. Zdálo by se, že není důvod zavádět jiné názvy do počtu pravděpodobnosti, ale není tomu tak. Důvodem je to, že slovo jev lépe odpovídá skutečnosti při aplikacích. A není třeba hovořit kostrbatě. Snadno mluvíme o jevu, že student je pohlaví mužského. Hůře se říká, že student je prvkem množiny studentů pohlaví mužského.
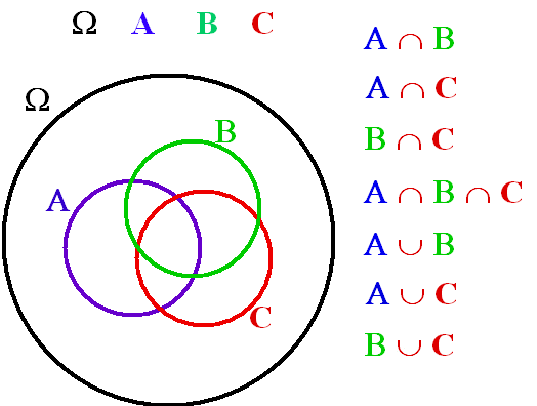
Odvození základních vzorců
Základní vzorce je možné si odvodit pomocí diagramů. Při přísně matematickém přístupu je však nutné je detailně dokazovat. Několik úvah je zde uvedeno, obvykle jsou výsledky známy a v běžném životě používány.
Vzorec pro doplněk
Pro množiny A a B definujeme jejich rozdíl A - B jako ty prvky z A, které nejsou v B.
Jestliže B `\subseteq `A, pak P(A)=P(A-B) + P(B).
Důkaz(použijeme diagram).
Můžeme psát A = (A-B)`\cup` B, což znamená, že A se skládá z těch prvků z A, které nejsou v B a z těch, které jsou v A ∩ B. To zároveň říká, že A - B a A ∩ B jsou disjunktní a tudíž P(A)=P((A-B) `\cup` B)=P(A-B)+P(B).
Důsledek pro doplněk.
Uvažujme jev jistý S. Každý jev je částí jevu jistého, proto P(S)=P(S-B)+P(B). Víme, že P(S)=1, takže dostáváme 1=P(S-B)+P(B) a P(S-B)=1-P(B).
Důsledek pro jev nemožný
Pravděpodobnost jevu nemožného je rovna 1-P(S) = 0.
V našem seznamu axiomů jsme zavedli to, že pravděpodobnost jistého jevu je jedna a z toho jsme právě vypočítali, že pravděpodobnost nemožného jevu je nula. Místo axiomu o pravděpodobnosti jistého jevu jsme mohli uvést axiom o pravděpodobnosti nemožného jevu a odvodit pravděpodobnost jistého jevu. Při tomto odvození je podstatný axiom o aditivnosti.
Aditivnost se týká disjunktních jevů. To není vždy ten případ, proto je dobré znát i vzorce pro pravděpodobnost sjednocení dvou jevů obecně.
Tvrzení.
Pro libovolné dva jevy A a B ze stejné základní množiny platí
P(A `\cup` B) =P(A-B)+P(B).
Důkaz.
Diagram je dobrou pomůckou, detaily by mohly vypadat takto. Jevy A-B a B jsou neslučitelné, proto platí P((A-B) `\cup` B)=P(A-B)+P(B). Musíme se ještě přesvědčit, že (A-B)`\cup` B = A `\cup` B. Je-li nějaký prvek v (A-B) `\cup` B, je buď v A-B nebo v B, tudíž je i v A `\cup` B. Obráceně, je-li nějaký prvek v A `\cup` B, je buď v B nebo v A-B, tudíž je v (A-B) `\cup` B.
Tvrzení.
Pro libovolné dva jevy A a B ze stejné základní množiny platí
P(A `\cup` B) =P(B-A)+P(A).
Důkaz se provede stejně jako u předchozího tvrzení. Na diagramu bychom opět viděli, že jsme neudělali nic jiného než zapsali A `\cup` B jako sjednocení neslučitelných jevů a tím můžeme použít aditivnost.
Tvrzení.
Pro libovolné dva jevy A a B ze stejné základní množiny platí
P(A `\cup` B) = P(A-B) + P(B-A) + P(A ∩ B).
Důkaz.
Z předchozího již víme, že P(A `\cup` B) = P(A-B) + P(B). Dále je B = (B-A) `\cup` (A ∩ B), což je sjednocení disjunktních množin, takže platí P(B) = P(B-A) + P(B ∩ A).
Tvrzení.
Pro dva libovolné jevy A a B ze stejné základní množiny platí P(A `\cup` B) =P(A)+P(B)-P(A ∩ B).
Důkaz.
Víme, že P(A `\cup` B)=P(A-B)+P(B-A)+P(A∩ B). Můžeme ale psát A=(A-B) `\cup` (A ∩ B) jako disjunktní sjednocení a P(A)=P(A-B)+P(A ∩ B). Odtud P(A-B)=P(A)-P(A ∩ B). Stejně odvodíme, že P(B-A)=P(B)-P(A ∩ B) a dosadíme.
P(A `\cup` B)=P(A-B)+P(B-A)+P(A ∩ B)=P(A)-P(A ∩ B)+P(B)-P(A ∩ B)+P(A ∩ B) = P(A)+P(B)-P(A ∩ B).
To byl formální důkaz, ale intuitivně si stačí pamatovat, že v součtu P(A)+P(B) se pravděpodobnost P(A ∩ B) načítá dvakrát, takže ke správnému výsledku dojdeme, když P(A)+P(B) upravíme odečtením P(A ∩ B).
Blok 0402 - Příklady - pravidla pro počítání s pravděpodobností
(Pro zobrazení odpovědi klikni na otázku.)
1) Jaká je pravděpodobnost, že v rodině se třemi dětmi jsou právě dva chlapci? Chlapci se rodí s pravděpodobností 0,52.