Úvod do problematiky
Rozdělení pravděpodobností-diskrétní náhodné veličiny
Náhodné veličiny
Náhodné jevy a náhodné veličiny
V předchozím výkladu o počtu pravděpodobnosti jsme se zabývali jevy, výsledkem experimentu byl tedy jeden z elementárních jevů. Další výklad o počtu pravděpodobnosti bude pokračovat tím, že výsledkem experimentu bude číslo. Jinak to lze říci i tak, že elementární jevy budou čísla. Tím se dostáváme k pojmu náhodná veličina.
Ten nejjednodušší příklad už jsme probírali. Je jím házení kostkou. Když nás přestane zajímat, která strana kostky padla, ale zajímá nás už jen číslo, které vyšlo, hovoříme o náhodné veličině. Tento posuv od toho, jakým způsobem došlo k odvození pravděpodobnosti směrem k tomu, že nás zajímá jen číslo a k němu přiřazené pravděpodobnosti je typický. Ve statistice se zabýváme hlavně čísly a náhodné veličiny jsou tím hlavním, co je potřebné k zvládnutí základních pojmů statistiky.
Náhodné veličiny se dělí na diskrétní a spojité. Jejich matematický popis je podstatně odlišný. Porovnání dvou veličin, z nichž jedna je diskrétní a druhá spojitá, je možné pomocí jejich distribučních funkcí, jež jsou obdobou kumulativních relativních četností. V tomto smyslu pak bude možné říkat jak dalece se diskrétní a spojité náhodné veličiny od sebe liší.
Pro názornost se někdy používá pojmu realizace náhodné veličiny. Tím je myšlen jeden experiment, jehož výsledkem je číslo. Z matematického hlediska je to prostě jedna náhodná veličina, ale pojem realizace se zavádí jen proto, aby bylo možné si představit něco konkrétnějšího. Jako jednoduchý příklad pro promyšlení by opět mohl posloužit hod kostkou.
Náhodné veličiny se zásadně označují velkými písmeny, typicky X, Y. Číselné hodnoty se označují písmeny malými. Například to, že náhodná veličina bude menší než číslo t se zapisuje jako P(X< t). Při přísně množinovém přístupu se jedná o pravděpodobnost jevu, že X< t tedy množinu elementárních jevů, jejichž hodnoty jsou menší než t, když si uvědomíme, že u náhodných veličin jsou elementárními jevy čísla.
Diskrétní náhodné veličiny
Diskrétními náhodnými veličinami rozumíme ty, které nabývají jen konečného nebo spočetného množství hodnot. Spočetné množství prvků znamená takové, že se dá očíslovat celými kladnými čísly. Množinu skládající se ze spočetného množství prvků lze po očíslování jejich prvků napsat jako posloupnost.
Všechna reálná čísla, ani intervaly, ať otevřené nebo uzavřené, skládající se z reálných čísel, nelze napsat jako posloupnost všech čísel v těchto intervalech. Tvoří tudíž množiny nespočetné.
Nejčastěji jsou studovány diskrétní náhodné veličiny, které nabývají konečného počtu hodnot, a to hodnot 0, 1, 2, …, N. Diskrétním náhodným veličinám, které nabývají konečného počtu hodnot, odpovídají ordinální data. Relativním četnostem v případě ordinálních dat budou odpovídat pravděpodobnosti u diskrétních náhodných veličin.
Pro popis diskrétní náhodné veličiny tedy už jen potřebujeme znát pravděpodobnosti, s jakými náhodná veličina jednotlivých hodnot nabývá. Tyto pravděpodobnosti označujeme P(X=K). Pokud je jasné, o kterou náhodnou veličinu jde, zjednodušíme si práci použitím zkráceného označení P(K).
Nejjednodušším popisem diskrétní náhodné veličiny je tabulka, ve které se uvedou hodnoty, kterých náhodná veličina nabývá a pravděpodobnosti.
0 P(0)
1 P(1)
2 P(2)
: :
: :
N P(N)
Principem tohoto způsobu zápisu je vyjmenování hodnot, čili elementárních jevů, a jejich pravděpodobností. Poznamenejme, že jestliže náhodná veličina nabývá jen hodnot 0 až N, musí být součet všech pravděpodobností roven jedné,
`\sum^N_{i=0} P (i)= 1`
neboť je to pravděpodobnost jevu jistého. Množinu hodnot, kterých nějaká náhodná veličina nabývá, si můžeme rozšířit, pak ale musíme prohlásit, že pravděpodobnosti hodnot, o které rozšiřujeme, jsou nulové.
Příklad: Házení ideální kostkou. Náhodná veličina takto vzniklá má tabulku
X P(X)
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6
Kdyby někdo chtěl definici od nuly, bude to
X P(X)
0 0
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
6 1/6
Binomické (Bernoulliovo) rozdělení
Alternativní rozdělení
Jestliže náhodná veličina může nabývat jen hodnot 0 a 1 s pravděpodobnostmi q a p nazývá se takové rozdělení alternativní. Musí platit q = 1 - p.
Uvedeme tabulku:
| hodnota | pravděpodobnost |
| 0 | q |
| 1 | p |
Protože se někdy ta čísla pletou, říká se, že číslo 1 je úspěch a číslo 0 je neúspěch.
Alternativní rozdělení tedy reprezentuje výsledek jednoho pokusu.
Pojem alternativní náhodné veličiny je jednoduchý a má mnoho použití. Hodí se nejen k modelování ordinálních dat, ale i nominálních, pokud se uvažují jen dvě kategorie, neboli ta druhá je doplňkem k první. Nehovoříme o kategorii prázdné a jisté.
Jen pro zajímavost se zmíníme o tom, že alternativní rozdělení se používá jako tak zvaná indikátorová funkce. Když v počtu pravděpodobnosti přiřadíme nějakému jevu A číslo jedna, čili jej prohlásíme za úspěch, použijeme pravděpodobnost P(A) tohoto jevu pro definici alternativního rozdělení. Když nastane jev A, je to označeno za úspěch, náhodná veličina nabývá hodnoty 1. Doplňku tohoto jevu se říká neúspěch - náhodná veličina nabývá hodnoty 0.
Obecně se pojem indikátorová funkce používá v teorii množin tak, že tato funkce zobrazuje prvky x množiny S na množinu skládající se jen ze dvou prvků 0 a 1. Pro podmnožinu A množiny S, indikátorová funkce IA(a) nabývá hodnoty 1, jestliže x je prvkem A a hodnoty 0, jestliže x není prvkem A. Tato konstrukce se může zdát umělou, ale plně vystihuje použití alternativního rozdělení.
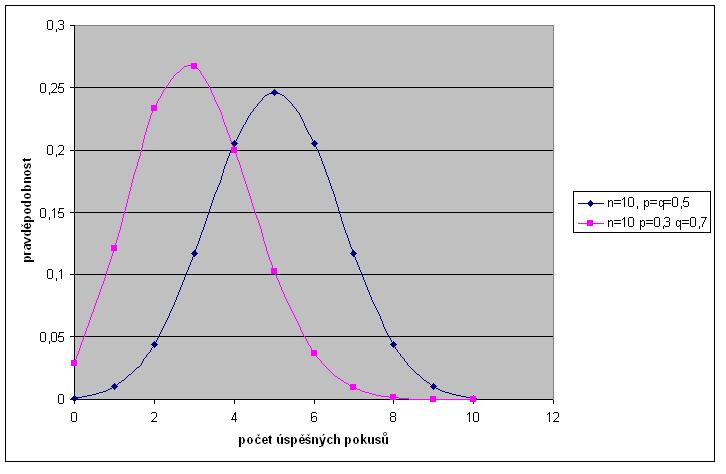
Graf binonického rozdělení pro N=10 a různé hodnoty p a q
Binomické rozdělení
Předpokládejme, že pravděpodobnost úspěchu v jednom experimentu je p a pravděpodobnost neúspěchu je q = 1 - p. Představme si, že provedeme nezávisle N experimentů. Při nich nám vyjde K úspěchů. Počet úspěchů K můžeme chápat jako náhodnou veličinu X, která může nabývat hodnot celočíselných od nuly maximálně do N.
Musíme pouze odvodit pravděpodobnosti. K tomu je podstatná podmínka nezávislosti. Zatím umíme odvodit pravděpodobnost P(X=N) toho, že při N experimentech nastane N úspěchů. Vyjdeme z nezávislosti a použijeme pravidlo o násobení, takže P(X=N) = pN.
Podobně umíme říci, že P(X=0) = qN. Zbývá jen odvodit obecný vzorec pro libovolné K. Když se řekne libovolné, je jasné, že pro K>N a pro K< 0 je pravděpodobnost nulová.
Začneme případem N=2. Zkratka NeNe znamená, že nastaly dva neúspěchy, NeUs označuje neúspěch a úspěch a tak dále. Díky nezávislosti můžeme pravděpodobnosti násobit, takže například pravděpodobnost neúspěchu následovaného úspěchem můžeme zapsat jako qp. Celý seznam možných výsledků dvou pokusů je i s jejich pravděpodobnostmi v následující tabulce.
NeNe qq
NeUs qp
UsNe pq
UsUs pp
Odtud vypočteme, že P(X=0) = q2, P(X=1) = qp + pq = 2pq, P(X=2) = p2. Je dobré si uvědomit, že u binomického rozdělení záleží jen na počtu úspěchů, nikoliv na pořadí, ve kterém se úspěchy a neúspěchy vyskytnou.
Mnohočlen, čili polynom, skládající se jen ze dvou členů, například p+q se nazývá binom. Známe vzorec (p + q)2 = p2 + 2pq + q2, u kterého si můžeme zkontrolovat, že dává jako sčítance pravděpodobnosti binomického rozdělení pro N=2.
Zkusíme si projít ještě všechny případy pro N=3. Dostaneme
NeNeNe qqq
UsNeNe pqq
NeUsNe qpq
NeNeUs qqp
UsUsNe ppq
UsNeUs pqp
NeUsUs qpp
UsUsUs ppp
Jelikož na pořadí nezáleží, neboť nás zajímá jen počet úspěchů, je P(X=0) = q3, P(X=1) = 3pq2, P(X=2) = 3p2q, P(X=3) = p3.
Tento přístup je možné zobecnit pro libovolný počet pokusů N. Výskyt úspěchů a neúspěchů při N pokusech je možné si představit jako N pozic, na které umístíme K krát symbol Ne. Nezáleží při tom na pořadí. Toto je ale známá otázka z kombinatoriky, kdy se ptáme, kolika způsoby můžeme vybrat K prvků z N prvků, když se prvky mohou opakovat. Počet způsobů je dán binomickým koeficientem
`\left( {_K^N}\right)`
Všimněme si, že název opět pochází z použití tohoto koeficientu pro binomy. Jestliže si někdo nepamatuje odvození, je možné tento koeficient chápat jen jako označení počtu způsobů výběru K pozic z N pozic.
`P(X=K)=\left({_K^N}\right)p^Kq^{N-K}`
Je jistě výhoda mít místo tabulek k dispozici jednoduchý vzoreček k počítání pravděpodobností. Pro úplnost je nutné dodat, že P(X=K) je nulová pro záporná K a pro K>N.
Poznámky k diskrétním náhodným veličinám
Jestliže pravděpodobnost úspěchu p i pravděpodobnost neúspěchu q je stejná, neboli p = q, a přitom q = 1 - p, tedy p = 1 - p, 2p = 1, potom musí platit p = 1/2. Tento model se často používá. Pro házení korunou, ale též když chceme říci, že zlepšení i zhoršení (nebo zvýšení či snížení) může nastat se stejnou pravděpodobností.
Blok 0405 - Příklady - diskrétní náhodná veličina
(Pro zobrazení odpovědi klikni na otázku.)
1) Pro binomické rozdělení platí:A) je charakterizováno průměrem a rozptylem,
B) závisí na počtu "úspěchů" v experimentu
C) toto rozdělení mohou mít i spojité náhodné veličiny
D) je součtem nezávislých alternativních rozdělení
2) Otázky ke zkoušce jsou rozděleny do tří skupin. Každá skupina obsahuje 20 otázek. Student si při zkoušce tahá z každé skupiny 1 otázku. Jaká je pravděpodobnost, že si student, který se naučil jen 15 otázek z každé skupiny, vytáhne alespoň 2 otázky, které se naučil?