Když provádíme přesná měření teploty kapalin nebo výpočty měrných tepelných kapacit látek při tepelné výměně, potřebujeme vždy vhodnou nádobu, která bude zabraňovat ztrátám tepla při našem měření. K podobným účelům se používá kalorimetr.

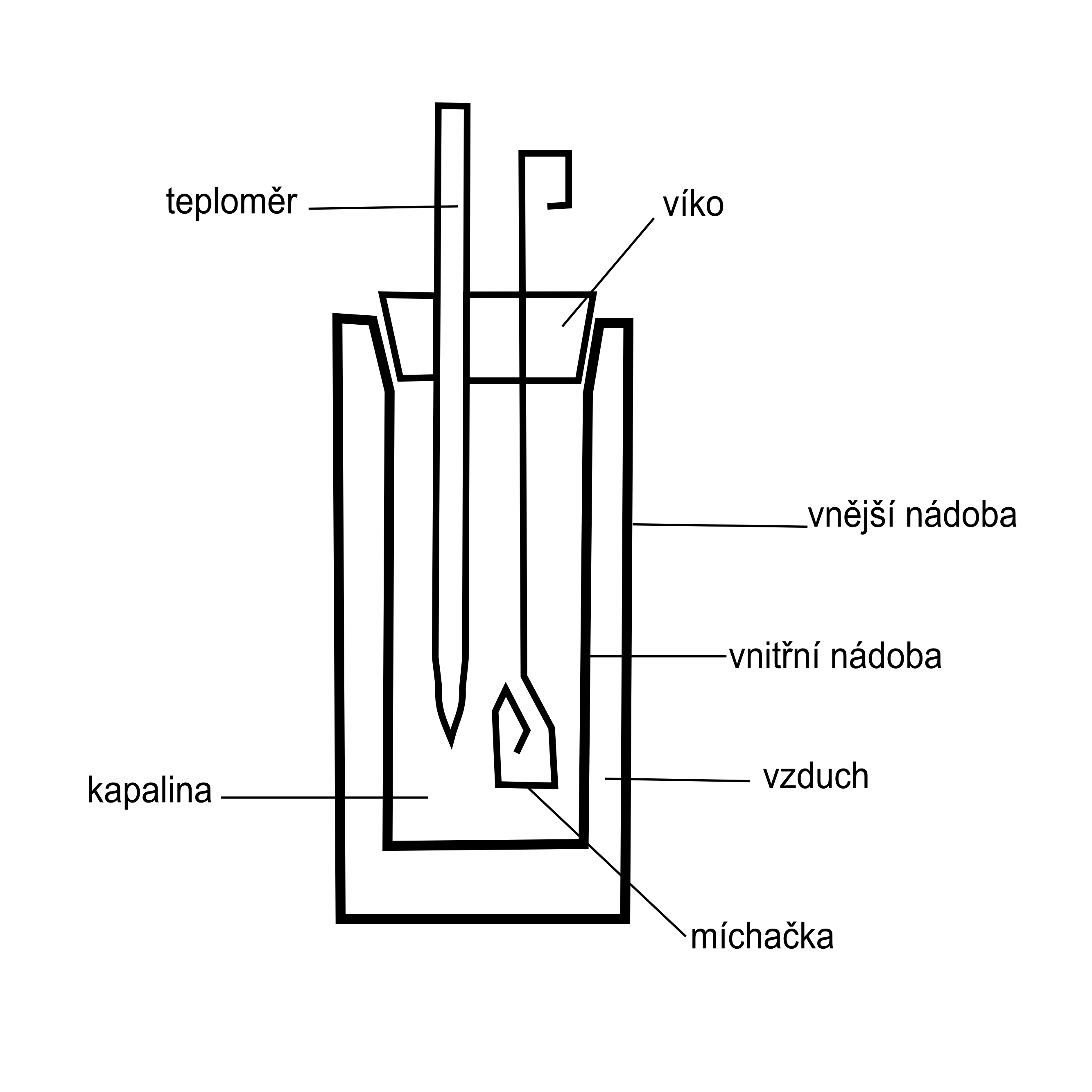
Směšovací kalorimetr je tepelně izolovaná nádoba s teploměrem a míchačkou. Aby se zabránilo únikům tepla, je menší nádoba vložena do větší, čímž se vytvoří kalorimetr s dvojitou stěnou. Vyleštění stěn, vzduchová vrstva nebo plastová izolace mezi nádobami, chrání prostor vnitřní nádoby před ztrátami tepla a také proti teplu vnikajícímu dovnitř z okolí. Míchačkou je možné pohybovat nahoru a dolů, nebo jí otáčet a jejím pohybem tak urychlit smísení dvou kapalin ve směs, jejíž teplotu potřebujeme měřit. Kalorimetr přikryjeme víkem, v kterém jsou otvory pro teploměr a míchačku.

Jak lze vypočítat měrnou tepelnou kapacitu tělesa z neznámého materiálu?

Jestliže do menší nádoby kalorimetru nalijeme např. vodu o hmotnosti m₁ a teplotě t₁, a ponoříme do ní váleček vyrobený z neznámého kovu o hmotnosti m₂ a teplotě t₂, nastane mezi oběma tělesy tepelná výměna, při které bude teplo z teplejšího válečku přecházet do vody. Na teploměru ponořeném ve vodě budeme pozorovat, že teplota vody poroste. Až se rtuť teploměru ustálí v jediné poloze, tepelná výměna mezi tělesy skončila a obě tělesa mají společnou teplotu t.
Při této tepelné výměně chladnější těleso (voda) přijalo teplo Q₁ od tělesa teplejšího (váleček) a zároveň můžeme říct, že teplejší těleso odevzdalo teplo Q₂ chladnějšímu. Protože v kalorimetru nedošlo k tepelným ztrátám do okolí, můžeme tento děj zapsat jako

`Q_1=Q_2`

Protože `Q_1=m_1*c_1*(t-t_1)` a současně `Q_2=m_2*c_2*(t_2-t)`, zapíšeme první rovnici ve tvaru tzv. kalorimetrické rovnice:

`m_1.c_1.(t-t_1 )=m_2.c_2.(t_2-t)`

Měrnou tepelnou kapacitu válečku z neznámého materiálu teď můžeme vypočítat ze vzorce

`c_2=\frac{m_1.c_1.(t - t_1 )} {m_2.(t_2-t)}`

Chceme-li získat přesnější výsledek měrné tepelné kapacity c₂ válečku z neznámého materiálu, nesmíme zapomenout, že teplem, které vydal neznámý váleček, se ohřála nejen voda, ale také vnitřní nádoba kalorimetru, míchačka a teploměr. Proto do kalorimetrické rovnice přidáme také tepelnou kapacitu kalorimetru, kterou označíme C_k. Přesnější kalorimetrická rovnice se potom zapíše ve tvaru:

`m_1.c_1.(t-t_1 )+C_K.(t -t_1 )=m_2.c_2.(t_2-t)`

`c_2=\frac{m_1.c_1.(t - t_1 )+ C_K.(t-t_1)} {m_2.(t_2-t) )`

ŘEŠENÉ ÚLOHY

Úloha č. 1

Zadání

Kolik vody o teplotě 50 °C musíme přidat do 600 l vody o teplotě 20 °C, aby vzniklá směs měla teplotu 30 °C? Tepelnou kapacitu nádoby zanedbejte.`.

`m_1 = 600 kg,`
`t_1 = 20 °C,`
`c_1 = c_2 = 4,2  {kJ}/{kg*K},`
`t_2 = 50 °C,`
`m_2 = ? kg`

Postup

Z daných veličin nejdříve musíme sestavit příslušnou kalorimetrickou rovnici.

`m_1.c_1.(t-t_1 )=m_2.c_2.(t_2-t)`

Neznámou veličinu `m_2` postavíme na jednu stranu kalorimetrické rovnice a všechny ostatní veličiny na opačnou stranu.

`m_2=\frac{m_1.c_1.(t - t_1 )} {c_2.(t_2-t)}`

Výsledek

`m_2=\frac{600*4200*10} {4200*20} = 300 kg = 300  l`

Do bazénu potřebujeme dolít 300 l vody o teplotě 50 °C.

Úloha č. 2

Zadání

O kolik K klesne teplota 10 l vody ohřáté na 80 °C, ponořil-li do ní student železné závaží o hmotnosti 2 kg a teplotě 293,15 K? Jakou výslednou teplotu bude mít železné závaží ?

`c_1 = 4,2  {kJ}/{kg*K},`
`c_2 = 0,450  {kJ}/{kg*K},`
`m_1 = 10  kg,`
`m_2 = 2  kg,`
`t_1 = 80 °C,`
`t_2 = 293,15  K = 20 °C,`
`t = ? °C`

Postup

`m_1*c_1*(t_1-t )=m_2*c_2*(t-t_2)`

`m_1* c_1 *t_1- m_1* c_1* t= m_2* c_2 *t- m_2* c_2* t_2`

`m_1* c_1 *t_1+ m_2* c_2 *t_2= m_1* c_1 *t+ m_2 *c_2* t`

`m_1* c_1 *t_1+ m_2* c_2 *t_2= t*(m_1*c_(1 )+ m_2 *c_2 )`

`t= (m_1* c_1 *t_1+ m_2* c_2 *t_2)/((m_1* c_(1 )+ m_2 *c_2 ) )`

`t = (10*4200*80+ 2*450*20)/((10*4200+ 2*450) )`

Výsledek

`t=78,74  °C`

Teplota 10  l vody klesne o 1,26 °C, čili o 1,26  K. Protože mezi tělesy proběhla tepelná výměna, bude mít po ustálení teplot také železné závaží teplotu 78,74 °C.

Protokol k laboratorní práci Určení měrné tepelné kapacity tělesa z neznámého materiálu si stáhněte z Moodlu na stránkách školy.

Kalorimetr a kalorimetrická rovnice

Testové otázky