Úvod
Obsah kapitoly
1.1 Energie Země
Pokud chceme využívat energii Země, měli bychom původ této energie znát. V této kapitole se velmi stručně seznámíme se vznikem sluneční soustavy, vznikem samotné planety Země a se zdroji energie, které na Zemi využíváme.
Vznik planety Země
Nejrozšířenější teorií o vzniku sluneční soustavy společně se Zemí je tzv. mlhovinová hypotéza, která předpokládá, že ve vesmíru existoval oblak složený z prachu a plynů, tzv. mlhovina. Mlhovina vznikla při výbuchu supernovy asi před 7 miliardami let obohacením mezihvězdného prachu o těžší prvky. Přibližně před 4,6 miliardami let došlo k výbuchu blízké hvězdy, tento výbuch byl spojený s tlakovou vlnou a část mlhoviny stlačil a uvedl do pohybu. Následkem výbuchu se tedy vytvořil hustší shluk, jenž se začal gravitační silou smršťovat. Částečky prachu a plynu se zformovaly do prstenců rotujících kolem hustého a hmotného středu mraku, do kterého byly postupně gravitační silou přitahovány další částice, zvyšovala se také jeho teplota. Jádro mračna se ohřálo natolik, že v něm začala probíhat termonukleární reakce a vzniklo Slunce. Společně se Sluncem se objevil sluneční vítr, který „odfoukl“ zbylý prach a plyn směrem ke vznikajícím planetám. Malé částečky v mračnu do sebe začaly narážet a spojovat se do stále větších kusů hmoty. Díky působení gravitace vznikaly stále rozsáhlejší a hmotnější objekty a nakonec celé planety, mezi nimi i původní Země, jejíž objem neustále rostl vlivem srážek s dalšími tělesy. Celý povrch Země byl pokryt krátery od dopadů těchto těles. S růstem planety se zvětšovala i její gravitace a přitahovala další, a také hmotnější tělesa. Díky tomu se zvětšovala nejen intenzita nárazů, ale také množství tepla, které při nich vznikalo. Další nárazy postupně tavily zemský povrch, který byl nakonec tvořen doruda rozžhaveným magmatem, který pokrýval celou planetu. Naše Země se dočasně proměnila ve žhavou kouli. Teploty na Zemi dosahovaly takových hodnot, že se od sebe začaly oddělovat jednotlivé prvky. Těžší prvky, jako např. železo a jiné kovy, klesaly ke středu, zatímco lehčí zůstávaly na povrchu. Tak došlo ke vzniku těžkého jádra, pláště a kůry, o jejíž vznik se zasloužily lehké prvky. Některá tělesa dopadající na Zemi obsahovala i vodu, která se odpařovala již při dopadu. Na rozdíl od kovů, které klesaly směrem ke středu, vodní pára spolu s jinými plyny a oxidem uhličitým stoupala vzhůru a vytvořila se hustá mračna. Kolem Země vznikla prvotní atmosféra. Počet dopadajících planetek na zemský povrch se postupně zmenšoval a povrch Země začal chladnout, současně začala klesat také teplota atmosféry. Když poklesla asi na 300 °C, přišel první déšť, na horký zemský povrch začala dopadat voda. Voda se okamžitě po dopadu vypařila, ve vyšších výškách opět kondenzovala a vytvářela další mraky. Cyklus se neustále opakoval, až se na Zemi vytvořily oceány.
Podobný proces probíhal pravděpodobně i na ostatních planetách zemského typu. Nedošlo zde ale ke vzniku oceánů, protože vlivy jako intenzivnější sluneční záření, slabší gravitace planety nebo vyšší teplota způsobily disociaci molekul vody a únik atomů vodíku do meziplanetárního prostoru.
Energie Země
Energie Země pochází ze dvou zdrojů. První zdroj je sluneční záření, které má sice rozhodující vliv na teplotu zemského povrchu, ale celkovou teplotu zemského tělesa prakticky neovlivňuje. Sluneční záření vzniká jadernými přeměnami v nitru Slunce. Energie je Sluncem vyzařována do všech směrů stejně a na naši planetu jí dopadá jen nepatrná část – pouze asi jedna dvoumiliardtina. Druhý zdroj energie Země pochází z dob jejího vzniku. Jedná se převážně o původní teplo akumulované v jejím nitru doplňované rozpady radioaktivních látek.
Zdroje energie obvykle dělíme na neobnovitelné a obnovitelné. Za neobnovitelný zdroj energie je obvykle považován takový zdroj energie, jehož vyčerpání je očekáváno v horizontu maximálně stovek let, ale jeho případné obnovení by trvalo mnohonásobně déle. Typickými příklady neobnovitelných zdrojů energie jsou především fosilní paliva: uhlí, ropa, zemní plyn a rašelina. Jejich energie opět pochází ze Slunce a byla ukládána v tělech rostlin a živočichů v průběhu jejich života. Dále sem patří jaderná energie, protože přirozené přírodní zásoby štěpných materiálů jsou také vyčerpatelné. Tato energie patří do druhé, menší části energie Země, která pochází z jejího nitra. Obnovitelný přírodní zdroj je takový, který má schopnost se při postupném spotřebovávání částečně nebo úplně obnovovat, a to sám nebo za přispění člověka. Typické příklady obnovitelných zdrojů jsou energie větru, energie slunečního záření, energie vody, energie půdy, energie vzduchu, energie biomasy a energie bioplynu, jejichž energie opět pochází ze Slunce. Do druhé skupiny obnovitelných energií patří geotermální energie.
Zpět na začátek1.2 Základní fyzikální pojmy
Stručný přehled fyzikálních pojmů, veličin a jednotek používaných v dalším textu.
-
Práce
charakterizuje děj, při kterém se přemísťují tělesa vlivem působení síly.
Urazí-li těleso působením konstantní síly o velikosti F dráhu s, přičemž síla je rovnoběžná s trajektorií, je práce
`bb W = F * S `Jednotkou práce je joule (J).
-
Výkon
popisuje, jak rychle se koná práce.
Průměrný výkon vypočítáme jako podíl práce W a doby t, za kterou byla práce vykonána, tedy
`bb P = W / T `
Jednotkou výkonu je watt (W). Ze vztahu pro výkon lze odvodit:
`bb P = W / T ⇒ W = P * t ⇒ [W] = W * s = J `Odtud vyplývá, že se pro práci může používat jednotka wattsekunda. Mnohem častěji se setkáváme s jejím násobkem kilowatthodinou. Platí:
-
Účinnost popisuje schopnost strojů využít dodanou energii E a přeměnit ji v užitečnou práci W, tedy
`bb η = W / E * 100% = P / P_0 * 100% `kde P je výkon a P0 příkon. -
Kinetická energie
hmotného bodu o hmotnosti m, který se pohybuje rychlostí v, je dána vztahem
`bb E_k = 1 / 2 mv^2 ` - Termodynamika a molekulová fyzika jsou části fyziky, které se společně zabývají teplotou a jejími změnami, tepelnou výměnou, vnitřní energií, změnou skupenství a podobně. Liší se pouze v přístupu ke zkoumaným tělesům. Termodynamika popisuje tělesa z tzv. makroskopického pohledu – vnímá je jako celek. Molekulová fyzika tělesa popisuje na základě jejich částicového složení.
-
Kinetická teorie stavby látek
je základem molekulové fyziky, obsahuje tři experimentálně ověřené poznatky:
- Látky všech skupenství se skládají z částic – částicemi rozumíme atomy, molekuly a ionty.
- Částice se v látkách neustále a neuspořádaně (chaoticky) pohybují – tento pohyb nazýváme tepelný pohyb, při vyšší teplotě se částice pohybují rychleji.
- Částice na sebe navzájem působí silami, tyto síly jsou při malých vzdálenostech odpudivé, při větších přitažlivé.
- Nultý zákon termodynamiky říká, že pokud jsou dvě tělesa při vzájemném dotyku v tepelné rovnováze, můžeme jim přiřadit stejnou teplotu. Tepelná rovnováha znamená, že se žádné z dotýkajících se těles neohřívá ani neochlazuje (tento stav bývá často nazýván rovnovážným stavem soustavy).
-
Celsiova teplota
t, jednotkou je Celsiův stupeň (°C). Celsiova teplotní stupnice má dva základní body:
- rovnovážný stav vody a ledu za normálního tlaku (101 325 Pa) – teplota tání ledu, dohodou jí přiřazujeme teplotu 0 °C,
- rovnovážný stav vody a její syté páry za normálního tlaku – teplota varu vody, dohodou jí přiřazujeme teplotu 100 °C.
-
Termodynamická teplota
T, jednotkou je kelvin (K). Termodynamická teplotní stupnice má jen jednu základní teplotu. Byla za ni zvolena teplota rovnovážného stavu soustavy
led, voda a sytá vodní pára. Tento rovnovážný stav se nazývá trojný bod vody a dohodou mu byla přiřazena teplota 273,16 K.
Převodní vztah mezi termodynamickou a Celsiovou teplotní stupnicí:
Převodní vztah mezi Celsiovou a termodynamickou teplotní stupnicí:
Termodynamická teplota 0 K je počátkem termodynamické teplotní stupnice. Libovolná soustava se k této teplotě může přiblížit, nemůže jí však dosáhnout. Proto se této teplotě říká absolutní nula. V blízkosti teploty 0 K (– 273,15 °C) se značně mění vlastnosti látek, např. elektrická vodivost. -
Vnitřní energie tělesa
je součet celkové kinetické energie neuspořádaně se pohybujících částic tělesa (atomů, molekul, iontů) a celkové potenciální energie vzájemné
polohy těchto částic.
Změna vnitřní energie souvisí se změnami kinetické energie částic, která závisí na rychlosti jejich pohybu. Znamená to, že při změně vnitřní energie
soustavy dochází ke změně její teploty. Vnitřní energii tělesa lze měnit:
- Konáním práce – např. třením nebo stlačováním plynu. Při tření se částice ležící na styčných plochách těles vzájemnými nárazy více rozkmitají a předávají pak část své energie dalším částicím uvnitř těles. Proto se zvětšuje teplota obou těles i jejich vnitřní energie. Při stlačování plynu roste teplota i vnitřní energie plynu.
- Tepelnou výměnou – děj, který nastává při dotyku těles o různých teplotách. Neuspořádaně pohybující se částice teplejšího tělesa při něm narážejí na částice dotýkajícího se studenějšího tělesa a předávají jim část své kinetické energie.
- Teplo Q je energie, kterou při tepelné výměně předá teplejší těleso studenějšímu, jeho jednotkou je joule (J).
- Zákon zachování energie: Při všech dějích probíhajících v izolované soustavě těles zůstává součet kinetické, potenciální a vnitřní energie těles konstantní.
-
Tepelná kapacita C tělesa
udává teplo, které musí těleso přijmout, aby se jeho teplota zvýšila o 1 °C (o 1K).
`bb C = Q / (Δt) `, ` [C] = J / K `
kde Q je teplo, které přijme těleso při zvýšení teploty o Δt. -
Měrná tepelná kapacita c
udává teplo, které musí přijmout 1 kg dané látky, aby se jeho teplota zvýšila o 1 °C.
`bb c = C / M = Q / (mΔt) `, ` [c] = J / (kg * K) `
kde Q je teplo, které přijme těleso o hmotnosti m při zvýšení teploty o Δt. Měrná tepelná kapacita je veličina charakteristická pro danou látku, poněkud se mění se změnou teploty, lze ji pro různé látky nalézt ve fyzikálních tabulkách, kde je uváděna obvykle pro teplotu 20 °C. Teplo, které přijme těleso, je přímo úměrné hmotnosti tělesa, měrné tepelné kapacitě tělesa a přírůstku jeho teploty:
-
Kalorimetrická rovnice
popisuje tepelnou výměnu mezi dvěma tělesy. Teplo, které jedno těleso odevzdá, se musí rovnat teplu, které druhé těleso přijme.
kde m1, c1, t1 je hmotnost, měrná tepelná kapacita a počáteční teplota prvního tělesa, m2, c2, t2 je hmotnost, měrná tepelná kapacita a počáteční teplota druhého tělesa, t je výsledná teplota těles po vyrovnání teplot.
-
První termodynamický zákon popisuje situaci, kdy se vnitřní energie současně mění konáním práce i tepelnou výměnou. Např. plyn v nádobě můžeme současně stlačovat a zahřívat stykem s teplejším tělesem.
-
Přírůstek vnitřní energie soustavy delta U se rovná součtu práce W vykonané okolními tělesy působícími na soustavu silami a tepla Q
odevzdaného okolními tělesy soustavě. Matematicky je tento poznatek vyjádřen rovnicí:
nebo
kde W´ = -W je práce plynu. -
Entalpie
H udává tepelnou energii uloženou v termodynamickém systému (pracovní látce). Entalpie, stejně jako vnitřní energie, je jedním z tzv.
termodynamických potenciálů, to znamená, že její úbytek udává práci, kterou termodynamický systém vykonal:
- Měrná entalpie h je entalpie pro 1 kg látky.
-
Stavová rovnice ideálního plynu
popisuje vztah mezi stavovými veličinami v libovolném rovnovážném stavu plynu.
kde p, V, T, N jsou stavové veličiny: p je tlak plynu, V je objem plynu, T je termodynamická teplota plynu a N je počet částic plynu. `bb k = 1.38 * 10^(-23) J * K^(-1) ` je Boltzmannova konstanta. -
Stavová rovnice ideálního plynu stálé hmotnosti
popisuje vztah mezi stavovými veličinami téhož plynu ve dvou různých stavech. První stav popisuje rovnice
`bb p_1V_1 = NkT_1 ⇒ (p_1V_1) / T_1 = Nk `
druhý stav popisuje rovnice
`bb p_2V_2 = NkT_2 ⇒ (p_2V_2) / T_2 = Nk `
počet částic N se nemění, jelikož se nemění hmotnost plynu. Z předchozích vztahů plyne
`bb (p_1 V_1) / T_1 = (p_2 V_2) / T_2 `
-
Izotermický děj s ideálním plynem
stálé hmotnosti je děj, při kterém se nemění teplota plynu. Platí stavová rovnice:
`bb p_1 V_1 = p_2 V_2 `
grafem izotermického děje v pV diagramu je izoterma. Při izotermickém ději je stálá teplota plynu, proto je stálá také vnitřní energie plynu. Teplo přijaté plynem při izotermickém ději je tedy rovno práci, kterou plyn vykoná:
a
-
Izochorický děj s ideálním plynem
stálé hmotnosti je děj, při kterém se nemění objem plynu. Platí stavová rovnice:
=
grafem izochorického děje v pV diagramu je izochora.
Při izochorickém ději je stálý objem plynu, proto plyn nekoná práci. Teplo přijaté plynem při izochorickém ději je tedy rovno přírůstku jeho vnitřní energie:
a
-
Izobarický děj s ideálním plynem
stálé hmotnosti je děj, při kterém se nemění tlak plynu. Platí stavová rovnice:
=
grafem izobarického děje v pV diagramu je izobara. Teplo přijaté plynem při izobarickém ději je rovno součtu přírůstku jeho vnitřní energie a práce, kterou plyn vykoná:
-
Adiabatický děj s ideálním plynem
stálé hmotnosti je děj, při kterém neprobíhá tepelná výměna mezi plynem a okolím. Pro adiabatický děj platí Poissonův zákon:
kde k je Poissonova konstanta, která závisí na druhu plynu. Pro plyny s jednoatomovými molekulami je přibližně 1,66, pro plyn s dvouatomovými molekulami asi 1,4. Grafem adiabatického děje v pV diagramu je adiabata. Při adiabatickém ději si plyn nevyměňuje teplo se svým okolím, proto je změna jeho vnitřní energie rovna práci vykonané okolními silami:
a
Při adiabatické kompresi (stlačování) plynu se teplota plynu zvyšuje. Při adiabatické expanzi (rozpínání) plynu se teplota snižuje. -
Kruhový děj
je děj, při kterém je konečný stav soustavy totožný s počátečním stavem. Grafem kruhového děje v pV diagramu je vždy uzavřená křivka.
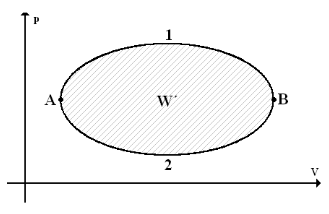
Obr. 1.1: Znázornění kruhového děje
- Práce W´ vykonaná během jednoho cyklu kruhového děje pracovní látkou je dána obsahem plochy uvnitř křivky zobrazující kruhový děj.
- Druhý termodynamický zákon říká, že nelze sestrojit periodicky pracující tepelný stroj, který by jen přijímal teplo od určitého tělesa (ohřívače) a vykonával stejně velkou práci.
-
Schéma cyklicky pracujícího tepelného stroje:
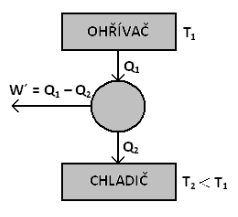
Obr. 1.2: Schéma cyklicky pracujícího tepelného stroje
Q1 je teplo přijaté pracovní látkou od ohřívače o teplotě T1, Q2 je teplo předané pracovní látkou chladiči o teplotě T2 a W´ je strojem vykonaná práce. -
Carnotův cyklus
popisuje funkci ideálního tepelného stroje, který převádí dodanou energii na užitečnou práci s maximální možnou účinností. Pro účinnost tepelného
stroje platí:

Chladnička je takový tepelný stroj, který využívá práce k čerpání tepla z chladnějšího prostředí do teplejšího, a to cyklickým vykonáváním vhodné posloupnosti dějů. V domácí chladničce koná práci elektrický kompresor a přenáší teplo prostřednictvím pracovní látky (chladicího média) z prostředí pro uskladnění jídla do místnosti. Ideální Carnotova chladnička je totéž co ideální Carnotův tepelný motor pracující pozpátku.
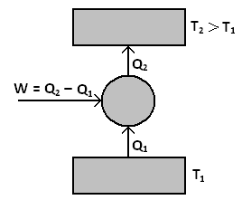
Obr. 1.3: Schéma chladničky a tepelného čerpadla
K popisu míry účinnosti (chlazení) používáme veličinu chladicí faktor:

Tepelné čerpadlo pracuje stejně jako chladnička, pouze s tím rozdílem, že teplo odebírané chladnějšímu (venkovnímu) prostředí využíváme pro vytápění. Jeho mírou účinnosti je topný faktor:

- Vypařování je změna skupenství látky z kapalného na plynné, probíhá při všech teplotách, jeho rychlost závisí především na teplotě kapaliny, druhu kapaliny, obsahu povrchu kapaliny a tlaku par nad kapalinou. Při vypařování kapalina odebírá teplo svému okolí.
- Skupenské teplo vypařování Lv je teplo, které musí kapalina přijmout, aby se přeměnila v páru téže teploty. Jednotkou této veličiny je joule (J).
-
Měrné skupenské teplo vypařování
lv je skupenské teplo vypařování pro 1 kg dané kapaliny. Tedy
`bb l_v = L_v / m `, `bb l_v = J / (kg) `
S rostoucí teplotou hodnota měrného skupenského tepla vypařování klesá. - Var kapaliny je zvláštní případ vypařování, při kterém se kapalina vypařuje nejen na svém povrchu, ale také uvnitř. Teplota varu kapaliny je závislá na vnějším tlaku. S rostoucím tlakem se zvyšuje.
- Kapalnění (kondenzace) je obrácený děj k vypařování.
- Sytá pára je pára, která je v rovnovážném stavu se svou kapalinou, což znamená, že počet molekul, který se za určitý čas vypaří, je stejný jako počet molekul, který za stejný čas zkapalní. V uzavřené nádobě v neměnných vnějších podmínkách se nad kapalinou vždy vytvoří sytá pára. Její tlak je určen druhem kapaliny a teplotou.