HMOTNOST ČÁSTIC
Všechna tělesa jsou složena z částic – atomů, iontů a molekul. Kdybychom znali počet částic v tělese, vynásobili bychom hmotnost jedné částice jejich počtem a nemuseli bychom těleso vážit, abychom poznali jeho hmotnost. Hmotnosti atomů a molekul jsou však tak malé, že bychom je nemohli na žádných vahách zjistit. Například atom nuklidu vodíku 1H má hmotnost 1,67355 . 10-27 kg. Proto ve fyzice a chemii používáme metodu porovnávání hmotností atomů nebo molekul s hmotností, kterou si zvolíme za základ.
Základem je `1/12` hmotnosti atomu uhlíku `_{6}^{12}C`, která se nazývá jako atomová hmotnostní jednotka mu a má přibližně velikost mu = 1,661 . 10-27 kg.
Relativní atomová hmotnost
Relativní atomová hmotnost je poměr hmotnosti daného atomu k atomové hmotnostní konstantě
(`1/12` hmotnosti atomu uhlíku `_{6}^{12}C`). Je to bezrozměrná veličina.
`A_r = m_a/m_u`
ma …. klidová hmotnost atomu,
mu…. atomová hmotnostní jednotka
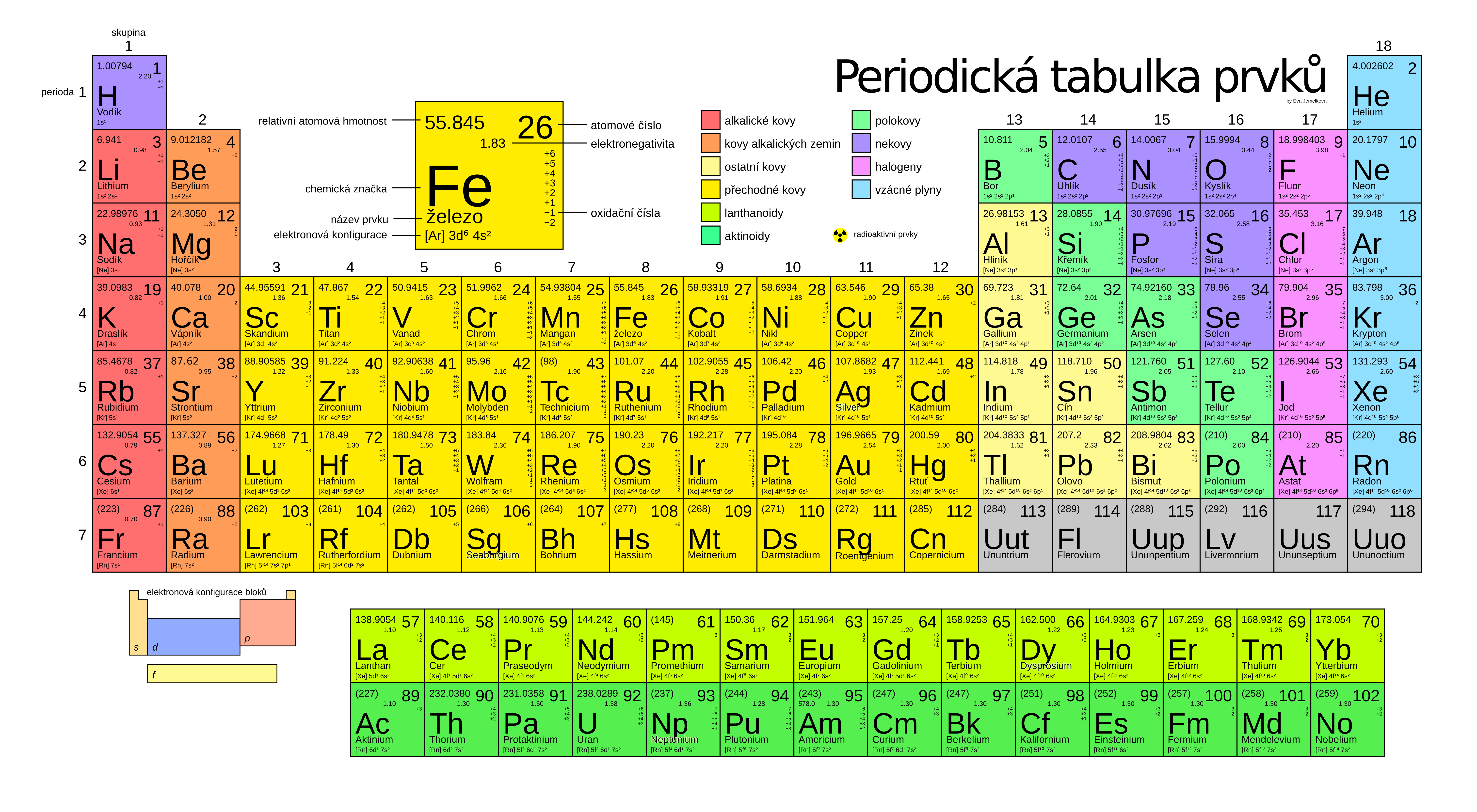
Najdeme ji u každého prvku uvedenou v periodické tabulce.
Relativní atomová hmotnost udává kolikrát je hmotnost atomu větší než atomová hmotnostní konstanta mu.
Pomocí relativní atomové hmotnosti daného prvku a atomové hmotnostní konstanty si můžete vypočítat klidovou hmotnost libovolného atomu nebo molekuly.
`m_a = A_r * m_u`
Řešená úloha
Vypočítej klidovou hmotnost atomu zinku, jestliže jeho relativní hmotnost Ar = 65,37.

Relativní molekulová hmotnost
Relativní molekulová hmotnost je poměr hmotnosti molekuly k `\frac {1}{12}` hmotnosti atomu uhlíku `_{6}^{12}C`. Je to bezrozměrná veličina.
`M_r = m_m/m_u`
mm …. klidová hmotnost molekuly,
mu…. atomová hmotnostní jednotka
Relativní molekulová hmotnost vyjádří, kolikrát je hmotnost molekuly větší než atomová hmotnostní konstanta mu.
Klidová hmotnost molekuly je rovna součtu klidových hmotností atomů, které molekulu tvoří.
Relativní molekulovou hmotnost můžeme také vyjádřit jako součet relativních atomových hmotností atomů, které tvoří molekulu.
Například relativní molekulovou hmotnost HNO3, zjistíme, když sečteme relativní atomové hmotnosti H, N a O, musíme ale vzít v úvahu, že kyslíku jsou v této molekuly tři atomy.
Řešená úloha
Vypočítej klidovou hmotnost molekuly HNO3.

LÁTKOVÉ MNOŽSTVÍ
Přímým měřením neumíme zjistit hmotnost atomů, ale neumíme ani experimentálně určit kolik částic je obsaženo v jakékoliv látce. Abychom mohli stanovit počty částic v různých látkách porovnáním se základní jednotkou počtu částic, byla zavedena veličina látkové množství n, jejíž jednotka je mol a dohodou bylo určeno, že jeden mol jakékoliv látky obsahule 6,023 . 1023 částic.
Počet částic v jednom molu látky udává Avogadrova konstanta NA.
Italský fyzik Amedeo Avogadro správně předpověděl, že stejné objemy všech plynů obsahují za stejného tlaku a stejné teploty stejné množství molekul. Například jeden litr těžkého plynu oxidu uhličitého obsahuje stejný počet molekul jako litr lehkého vodíku.
Říkáme, že jakákoliv látka má látkové množství 1 mol, když obsahuje právě tolik částic, kolik je obsaženo atomů ve 12 g nuklidu uhlíku `_{6}^{12}C`. Taková látka, aby měla látkové množství 1 mol, musí obsahovat 6,023 . 1023 částic.
Látkové množství n libovolné látky je rovno podílu počtu částic této látky N a Avogadrovy konstanty NA.
`n = \frac {N} {N_{A}}`
Molární veličiny
Veličiny, které se vztahují k látkovému množství příslušné látky, nazýváme molární veličiny. Často ve fyzice používáme molární hmotnost a molární objem.
Molární hmotnost definujeme jako podíl hmotnosti dané látky a jejího látkového množství. Vyjadřuje nám, jaká hmotnost připadá na jeden mol látky.
Vypočítáme ji ze vztahu `M_m = \frac {m} {n}`. Její jednotkou je kg . mol-1.
Molární hmotnost můžeme také vypočítat z relativní atomové nebo molekulové hmotnosti.
`M_m = A_r * 10^{-3} kg * mol^{-1}, M_m = M_r * 10^{-3} kg * mol^{-1}`.
Molární objem definujeme jako podíl objemu dané látky a jejího látkového množství. Vyjadřuje nám, jaký objem připadá na jeden mol látky, závisí na teplotě a tlaku. Vypočítáme ho ze vztahu `V_m = \frac {V}{n}`. Jeho jednotkou je m3 . mol-1.
Pro plyny byla za normální teploty 0°C a normálního tlaku 101,325 kPa stanovena hodnota normálního molárního objemu. Je to objem, který je za výše uvedených podmínek pro všechny plyny stejný. Jeho hodnota byla určena Vm = 22,414 dm3 . mol-1.
Řešené úlohy
Úloha č. 1
Úloha č. 2 
 Hmotnost částic a látkové množství
Hmotnost částic a látkové množství