Obsah kapitoly
2 Součásti k přenosu otáčivého pohybu
2.1 Hřídelové čepy
- části hřídelí, pomocí kterých je hřídel uložena v ložisku (resp. v rámu stroje). Z toho důvodu jsou na hřídelové čepy kladeny vysoké nároky, co se týká kvality povrchu a přesnosti rozměrů (ve stykových plochách vzniká tření a dochází k jejich opotřebení). Pro zvýšení tvrdosti stykových ploch mezi čepem a ložiskem je často tato část hřídele povrchově kalena, cementována, nitridována apod.
Každá rotující hřídel musí být uložena alespoň ve dvou ložiskách. Proto tedy má minimálně dva hřídelové čepy.
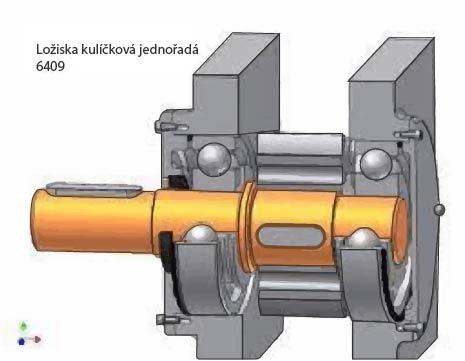
Obr. 1 Hřídel uložená v ložiskách
Druhy hřídelových čepů
- Podle směru zatěžující síly:
- radiální – přenáší síly, které působí kolmo na osu hřídele
- axiální – přenášejí síly působící v ose hřídele
- Podle tvaru a umístění na hřídeli:
Radiální čepy
- Válcové – nejběžnější provedení, ukládají se do radiálních ložisek (kluzných i valivých)
- čelní – vytvořeny na konci hřídele
- krční – vytvořeny na hřídelích s převislými konci, ale i ve střední části u hřídelí, uložených na více než dvou podporách (pak je nutné použít dělený náboj).
- Kuželové – mají tvar komolého kužele, z konstrukčních důvodů musí být umístěny vždy na konci hřídele. U kuželových čepů je nutné správně volit velikost kuželovitosti. V případě malého úhlu hrozí samosvornost hřídele v rámu stroje a k jeho zničení. V případě velkého úhlu kužele vznikají nežádoucí přídavné axiální síly (vlivem rozkladu sil ve stykové ploše). Kuželový radiální čep zajišťuje hřídel proti osovému posunutí v jednom směru.
- Prstencové – velmi malé využití, složitá výroba, použití možné pouze v kluzných ložiskách, malé opěrné plochy – přenášejí jen malé zatížení.
- Kulové – přenášejí zatížení v libovolném směru, výrobně nejnáročnější. Použití v zařízeních, ve kterých v průběhu činnosti mění zatížení svůj směr (např. náprava automobilu – průjezd zatáčkou, nerovnosti vozovky apod.).
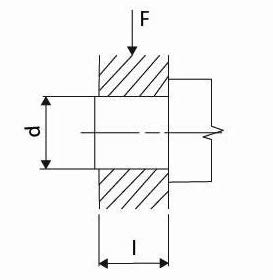
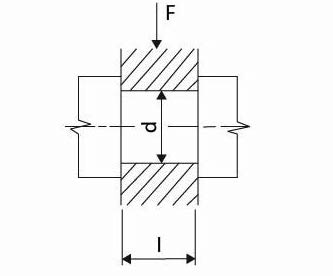
Obr. 2 Válcový čep
vlevo čelní, vpravo krční
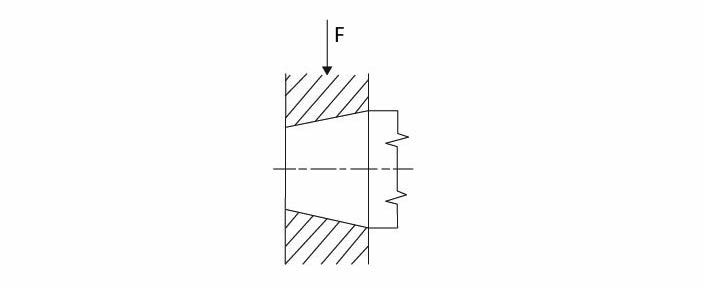
Obr. 3 Kuželový čep
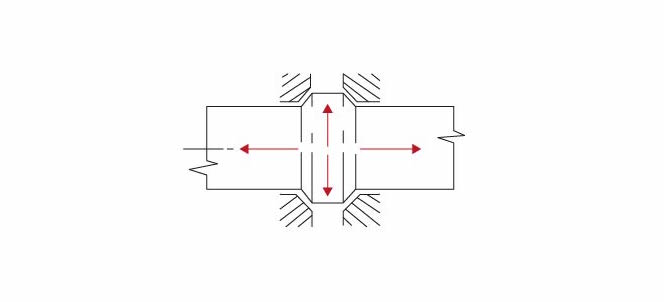
Obr. 4 Prstencový čep
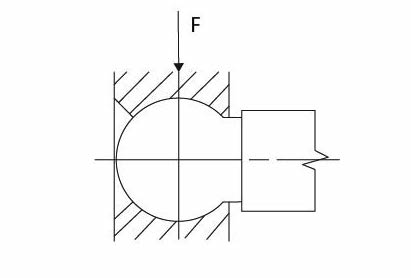
Obr. 5 Kulový čep
Axiální čepy
- Nožní (patní) – zachycují silového zatížení ve svislém směru. Obvykle je to vlastní tíha konstrukce, strojního zařízení, tíha břemene. Střední část kluzné plochy je vybrána pro zlepšení kluzných vlastností čepu. Je to proto, že v této části se nemůže vytvořit mazací olejový film, protože kluzná rychlost je v blízkosti středu čepu velmi malá. Čep by se ve střední části zadíral. Patní hřídelový čep má rovinnou kluznou plochu ve tvaru mezikruží. Ukládá se do kluzných axiálních ložisek.
- válcové – pro malé tlaky, čep je kalený, opírá se o kalenou podložku
- kuželové
- kulové – samostavitelné, velká třecí plocha.
- Prstencové
- Hřebenové – výrobně obtížné a drahé, nutná velká přesnost výroby nákružků. Možné obousměrné zatížení. Zatížení je stejnoměrné.

válcový kuželový kulový Obr. 6 Nožní čep
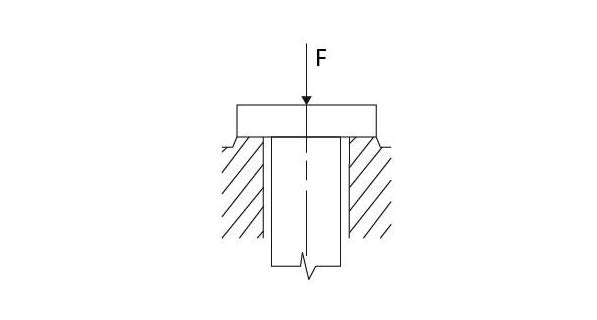
Obr. 7 Prstencový čep
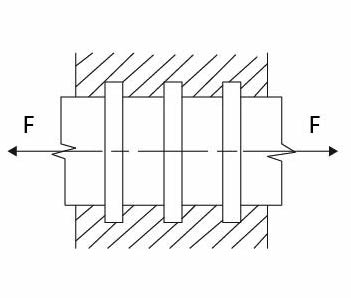
Obr. 8 Hřebenový axiální čep
- Válcové – nejběžnější provedení, ukládají se do radiálních ložisek (kluzných i valivých)
Výpočet radiálních čepů nosných hřídelí
Rozměry radiálního čepu stanovíme tak, aby byla zajištěna pevnost, provozní spolehlivost a životnost radiálních čepů.
U nosných hřídelů nejsou čepy namáhány krouticím momentem. Pevnostní návrhový výpočet se provádí pro namáhání ohybem. Dále je třeba provést kontrolu na otlačení a dle druhu použitého ložiska i kontrolu na oteplení.
Pevnostní návrhový výpočet – namáhání ohybem
σ_O = \frac {M_O} {W_O} ≤ σ_{DO}
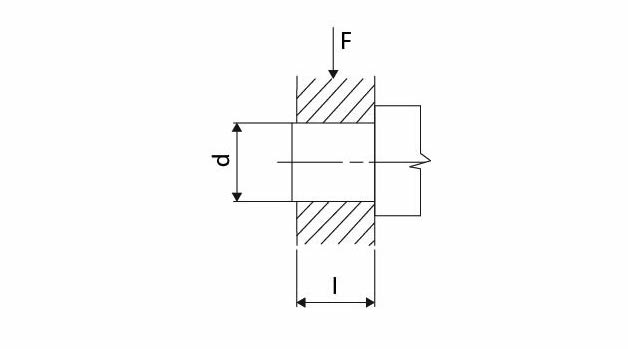
Obr. 9 Zatížení radiálního hřídelového čepu
Maximální ohybový moment:
M_{Omax} = F * l/2
Modul průřezu v ohybu pro kruhový průřez (pro jiné průřezy viz STAB):
W_O = \frac {πd^3} {32}
Pak:
σ_{DO} = \frac {M_{Omax}} {W_O} = \frac {F * l/2} {\frac {πd^3} {32}} ⇒ d = \root 3 {\frac {16 * F * l} {π * σ_{DO}}}
Kontrolní výpočet – otlačení
p = F/S = \frac {F} {l * d} ≤ p_D
Kontrola na oteplení (Kontrola provozní spolehlivosti)
Při velkých otáčkách čepu a velkém zatížení hrozí vznik velkého množství tepla, zahřátí čepu a následně pak i k jeho zadření. Množství tepla, vzniklé při otáčení čepu v kluzném ložisku, závisí na velikosti zatížení a velikosti kluzné rychlosti čepu.
p * v = \frac {F} {l * d} * π * d * n ≤ (p * v)_D
Použité veličiny:
F
\text{M}_{Omax}
\text{W}_O
d
n
v
\text{p}_D
\text{σ}_{DO}
zatěžující síla
maximální ohybový moment čepu
modul průřezu v ohybu
průměr čepu
otáčky hřídele/ložiska
obvodová rychlost (v = π * d * n)
dovolený tlak
dovolené napětí v ohybu
Štíhlost čepu
V pevnostních rovnicích jsou oba rozměry čepu, tzn. průměr d a délka l. Jeden, někdy i oba, je tedy nutné zvolit. Pro správnou funkci ložisek je důležitým ukazatelem jejich poměr:
λ = l/d
U radiálních čepů bývá tento poměr roven 0,3 až 1 (výjimečně 1,5).
Vztah pro výpočet štíhlosti čepu získáme i dělením vztahů pro σDO a pD:
\frac {σ_{DO}} {p_D} = \frac {{16 * F * l} / {π * d^3}} {{F} /{d * l}} = \frac {16 * l^2} {π * d^2} ⇒ λ = \sqrt \frac {π * σ_{DO}} {16 * p_D}
Výpočet axiálních čepů
Kluzná rychlost axiálních čepů roste směrem k obvodu nosné plochy (obr. a). Díky tomu na obvodu dochází k většímu opotřebení než uprostřed. Zaběhaná plocha je mírně klenutá, v okolí osy čepu nadměrně stoupá tlak a dochází k zadírání čepu. Tento nedostatek lze odstranit vybráním střední části čepu (obr. b).
Při návrhu těchto čepů se provádí kontrola na otlačení a oteplení (provozní spolehlivosti).
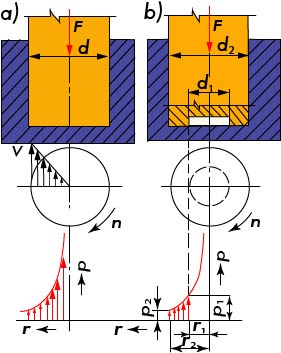
Obr. 10 Průběh rychlostí a tlaku u nožního čepu
a – čep nevylehčený, b – čep v ose vylehčený
Kontrola na otlačení
Největší tlak bude na poloměru r1
p_{max} = p_1 = \frac {F} {2π * (r_2 - r_1) * r_1} ≤ p_D
Průměr styčné plochy:
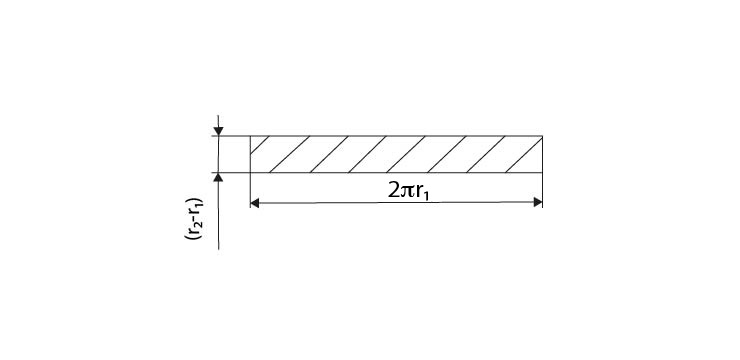
Obr. 11 Průmět styčné plochy
Kontrola na oteplení:
p_s * v_s ≤ (p * v)_D
v_s = π * d_s * n = π * \frac {d_1 + d_2} {2} * n
Střední tlak:
p_s = \frac {F} {1/4 π (d_2^2 - d_1^2)} ≤ p_D
Použité veličiny:
F
\text{d}_1
\text{d}_2
\text{d}_s
n
\text{p}_{max}
\text{p}_s
\text{p}_D
\text{r}_1
\text{r}_2
\text{v}_s
zatěžující síla
vnitřní průměr čepu
vnější průměr čepu
střední průměr čepu
otáčky hřídele/ložiska
maximální tlak
střední tlak
dovolený tlak
vnitřní poloměr čepu
vnější poloměr čepu
střední obvodová rychlost (v_s = π * d_s * n)
Zpět na začátek
Použitá literatura:
R. Kříž a kol. Stavba a Provoz strojů strojů I. SNTL – Nakladatelství technické literatury. 1977