Obsah kapitoly
2 Součásti k přenosu otáčivého pohybu
2.2 Hřídele
Hřídele jsou základní strojní součásti obvykle válcového tvaru, které umožňují nebo přenášejí rotační pohyb. Jsou na nich umístěna ozubená kola, kladky, páky, spojky, ruční kliky apod.
Materiál hybných hřídelí je volen podle požadované hmotnosti, opotřebitelnosti, možnosti tepelného zpracování, vrubové citlivosti, provozního zatížení: oceli 11 423, 11 500, 11 600, ušlechtilé (12), slitinové (13 až 17) – pro více namáhané hřídele určené zpravidla k zušlechťování 12 040, 12 050, 14 240, 15 240, 16 240, 16 440.
Podle druhu zatížení dělíme hřídele na:
- Nosné – nepřenáší pohyb a výkon, pouze nesou zátěž. Jsou namáhány na ohyb.
Dělíme je na:
- nehybné – jsou uloženy pevně v rámu stroje (zajištěny proti otáčení) a nesou otáčející se součást např. kladku, pojízdná kola kolejových vozidel apod.
- otáčivé – s pevně nalisovanými nebo naklínovanými koly. Nejsou namáhány na krut. Otáčejí se, pokud působí tažná síla. Např. nápravy železničních vagónů.

Obr. 1 Pojezdová kola na nábytek
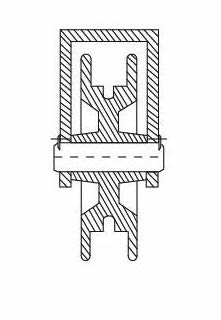
Obr. 2 Kladka na nosné hřídeli
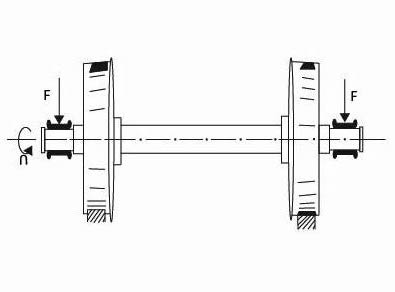
Obr. 3 Otáčivý nosný hřídel
- Hybné – přenášejí otáčivý pohyb a krouticí moment z místa pohybu do místa pracovního. Jsou tedy nuceně poháněny. Aby mohlo dojít k jejich pohybu, musí být uloženy v kluzných nebo valivých ložiskách. Jsou namáhány na krut (tam, kde přechází moment z jedné součásti do druhé, např. mezi ozubenými koly), popř. na krut a ohyb v případě, že nelze zanedbat hmotnost samotné hřídele a nesených součástí.
- přímé
- hladké
- osazené
Obr. 4 Osazený hřídel
- duté – mají mezikruhový průřez, výrobně velmi nákladné, v případě stejného průměru jako plné hřídele mají větší tuhost. Použití – např. vřeteno soustruhu, pohon lodních šroubů (dlouhé hřídele).
- klikové – pro víceválcové pístové stroje (spalovací motory, čerpadla, pístové kompresory).
Za každým zalomením následuje uložení hřídele v ložisku. Výrobně náročné, buď z
jednoho kusu odléváním nebo kováním, popř. složené z několika kusů.
Obr. 5 Klikový hřídel
- ohebné (flexibilní) – použití v případě, kdy je potřeba měnit polohu hnacího hřídele vzhledem k hnanému (pohon ručního mechanizovaného nářadí)

Obr. 6 Ohebný hřídel
- navíjení ohebného hřídele – na střední drát je vždy v opačném směru navinuto ve šroubovici 5 až 6 vrstev drátů. Poslední vrstva je navinuta ve smyslu otáčení hřídele. Pokud se hřídel otáčí v protisměru, jeho únosnost klesá o 20 až 50 %. Je tedy nutné, aby byl směr otáčení na hřídeli vyznačen
- ochranné hadice ohebného hřídele – jsou na hřídeli nasazeny s vůlí 1 až 2 mm, která je vyplněna tukem
- ochranné hadice ohebného hřídele – jsou na hřídeli nasazeny s vůlí 1 až 2 mm, která je vyplněna tukem
- drážkové

Obr. 7 Drážkový hřídel s evolventním drážkováním
- spojovací
- hnací
- předlohové
- hnané
- vačkové – osazené vačkami, v závislosti na svém pootočení ovládají posun strojních součástí (např. ovládaní ventilů ve spalovacím motoru).
Rozdělení hybných hřídelů podle tvaru
Rozdělení hybných hřídelů podle funkce

Obr. 8 Vačkový hřídel

Obr. 9 Schéma převodovky
(Os – spojovací hřídel, O1 – hnací hřídel, O2 – předlohový hřídel, O3 – hnaný hřídel)
Výpočet nosných hřídel
Otočný nosný hřídel s nalisovaným kolem – zatěžující síla působí uprostřed
- příkladem je uložení kladky
- provede se návrhový výpočet průměru hřídele z pevnostní rovnice na ohyb a kontrolní výpočet na otlačení pod kotoučem a v ložiskách rámu.
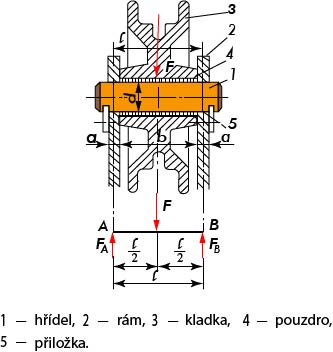
Obr. 10 Uložení kladky - Nehybný nosný hřídel uložený na obou koncích, zatížený silou uprostřed
Postup výpočtu:
Výpočet na ohyb
- Stanovení reakcí v podporách A, B
F_A = F_B = 1/2 F
- Výpočet maximálního ohybového momentu (uprostřed)
M_{Omax} = F_A * 1/2 * l = F_B * 1/2 * l = F/2 * l/2 = \frac {F * l} {4}
- Návrh průměru hřídele z maximálního ohybového napětí
σ_O = \frac {M_{Omax}} {W_O} ≤ σ_{DO}, W_{O} = \frac {πd^3} {32}
σ_{DO} = \frac {M_{Omax}} {W_O} =\frac {32 * F_A * l} {2 * π * d^3} ⇒ d = \root 3 \frac {16 * F_A * l} {π * σ_{DO}} = \root 3 \frac {32 * M_O} {π * σ_{DO} }
Výpočet na otlačení – otlačení nesmí překročit danou hodnotu závislou na materiálu náboje a obvodové rychlosti.
Tlak pod kotoučem (b se buď volí, nebo vypočítá pomocí p_D)
p = F/S = F/{b * d} ≤ p_D
Tlak v ložiskách rámu (a se buď volí, nebo vypočítá pomocí p_D)
p = F/S = F/{2 * a * d} ≤ p_D
Použité veličiny:
F
\text{F}_A, \text{F}_B
\text{W}_o
\text{M}_o
\text{p}_D
d
\text{σ}_{DO}
zatěžující síla
reakce v podporách
modul průřezu v ohybu
maximální ohybový moment
dovolený tlak
průměr hřídele
dovolené napětí v ohybu
Otočný nosný hřídel s nalisovaným kolem – zatěžující síla nepůsobí uprostřed
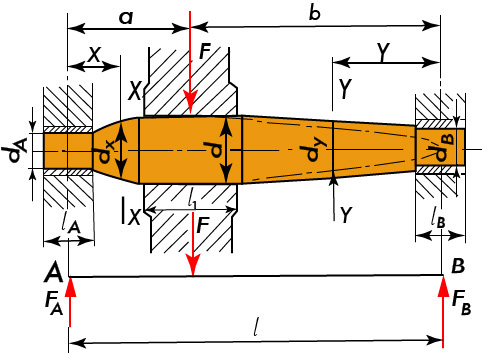
Obr. 11 Otočný nosný hřídel s nalisovaným kolem – zatěžující síla nepůsobí uprostřed
Postup výpočtu:
Výpočet na ohyb
- Výpočet reakce v podporách A, B
Z rovnováhy momentů: \text \sum \text {M}_A = 0 ⇒ F * a - F_B * l = 0 ⇒ F_B = \frac { F * a} {l}
nebo
\text \sum \text {M}_B = 0 ⇒ F_A * l - F * b = 0 ⇒ F_A = \frac {F * b} {l}
Z rovnováhy sil:
\text \sum \text {F}_y = 0 ⇒ F_A - F + F_B = 0 ⇒ F_A = F - F_B
- Výpočet maximálního ohybového momentu (pod kolem)
M_o = F_A * a = F_B * b = {F * b * a} / {l}
- Výpočet průměru d hřídele z největšího ohybového napětí
σ_O = {M_O} / {W_O} ≤ σ_{DO}; W _{O} = \frac {πd^3} {32}
pak
σ_{DO} = \frac {M_O} {W_O} = \frac {F_A * a} {{πd^3}/{32}} ⇒ d = \root 3 \frac {32 * F_A * a} {π * σ_{DO}}
Kontrola na otlačení – z otlačení se vypočítá délka náboje l1
- Pod kotoučem
p = F/S = F /{l_1 * d} ≤ p_D
-
V ložiskách
p_1 = p_A = {F_A} / {S_1} = {F_A} / {l_A * d_A} ≤ p_D
p_2 = p_B = \frac {F_B} {S_2} = \frac {F_B} {l_B * d_B} ≤ p_D
Výpočet hybných hřídelí
Typy a namáhání hybných hřídelí

Obr. 12 Typy a namáhání hybných hřídelí
a) Spojovací hřídel; b) hnací a hnaný hřídel; c) předlohový hřídel
Výpočet na krut
Pevnostní rovnice:
τ_k = \frac {M_k} {W_k} ≤ τ_{Dk}
Krouticí moment:
M_k = \frac {P} {\omega} [N * m], P [W] ...přenášený výkon
Úhlová rychlost:
\omega = 2 * π * n ⇒ n [s^{-1}], \omega = \frac {π * n} {30} ⇒ n [min^{-1}]
Modul průřezu v krutu (viz STAB):
W_k = \frac {π} {16} * d^3 ≅ 1/5 d^3
Výpočet průměru hřídele d:
τ_{DK} = \frac {M_k} {W_k} = \frac {M_k} {1/5 d^3} ⇒ d = \root 3 \frac {5 * M_k} {τ_{DK}} nebo d = \root 3 \frac {5 * P * 10^3} {τ_{DK} * \omega}
Výpočet na tuhost v krutu (úhel zkroucení)
U štíhlých dlouhých hřídelí nedojde k jejich porušení v důsledku překročení meze kluzu, ale v důsledku trvalé deformace (zkroucení).
Úhel zkroucení:
φ = \frac {M_k * l} {G * J_p} [rad]
Pro úhel zkroucení ve stupních:
φ = \frac {M_k * l} {G * J_p} * \frac {180} {π} [°]
φ
l
\text {J}_p
\text {M}_k
G
úhel zkroucení
délka hřídele, [mm]
polární moment krutu, [\text {mm}^4]
krouticí moment [\text{N} * \text{mm}]
modul pružnosti materiálu ve smyku, [MPa], pro ocel \text {G} =\text {8} * \text {10}^4 MPa
Polární moment průřezu v krutu:
– pro kruhový průřez
J_p = π/32 * d^4 ≅ 1/10* d^4 [\text{mm}^4]
– pro mezikruhový průřez
J_p = π/32 * (D^4 - d^4) ≅ 1/10 (D^4 - d^4) [\text{mm}^4]
Výpočet průměru hřídele d (dosazením do deformační rovnice):
J_p = 1/10 * d^4
φ = \frac {10 * M_k * l} {G * d^4} * \frac {180} {π} ⇒ d = \root 4 \frac {10 * M_k * l * 180} {π * φ * G} [\text{mm}]
Pozn.: φ dosazujeme ve [°]
Obvykle je dovoleno poměrné zkroucení (zkrut):
\nu = φ/l = 0,25 \text{až} 1, \text {výjimečně 1,5} = [° * m]
Pozn.: v tomto případě dosazujeme délku hřídele v [m].
Výpočet na ohyb (Obr. 12 Typy a namáhání pohybových hřídelí b), c))
Zatěžující síly:
F_1 = \frac {2M_k}{D_1}, F_2 = \frac {2M_k} {D_2}
Maximální ohybový moment (Obr. b))
M_{Omax} = F_B * a nebo M_{Omax} = F_A * l_1
Maximální ohybový moment (Obr. c))
M_{Omax} = F_B * a
Z velikosti zatěžujících sil, rozpětí ložisek a polohy ozubených kol na hřídeli vypočteme z momentové věty reakce FA a FB. Z obrazce posouvajících sil (Schwedlerova věta) zjistíme, kde je \text {M}_{Omax}.
Výpočet na kombinované namáhání (ohyb + krut, Obr. b), c))
Redukovaný ohybový moment:
M_{RED} = \sqrt {M_{Omax^2} + 0,75 (α_B * M_k)^2} [\text{N} * \text{mm}]
Průměr hřídele v nebezpečném průřezu:
d = \root 3 \frac {10 * M_{RED}} {σ_{DO}}
α_B
Bachův opravný součinitel dle druhu namáhání (viz STAB)
α_B = 0,4 – střídavý ohyb a klidný krut
α_B = 0,7 – střídavý ohyb a míjivý krut
α_B = 1 – střídavý ohyb a střídavý krut
Výpočet dutých hřídelí
Z obrázku je patrné, že k pevnostnímu využití materiálu dochází pouze na povrchu hřídele, protože průměr hřídele se navrhuje pro největší napětí. Materiál je tedy pevnostně lépe využit u dutých hřídelí. Zároveň dojde ke snížení hmotnosti hřídele. Pokud je hmotnost hřídele provrtáním snížena na polovinu, jeho pevnost se sníží pouze o čtvrtinu.
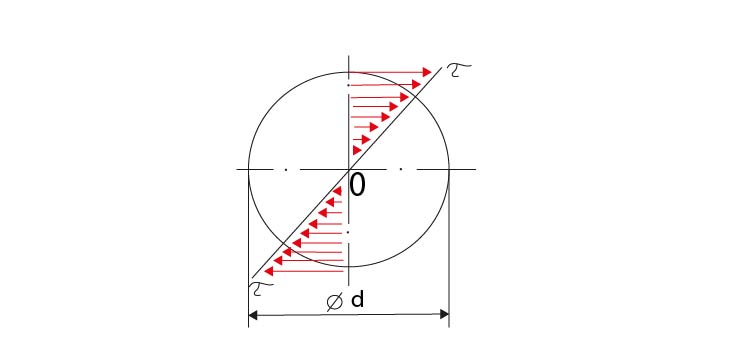
Obr. 13 Rozložení tangenciálních napětí hřídelů namáhaných krutem
U dutých hřídelí se provádí kontrola napětí v krutu τ_kze základní pevnostní rovnice pro krut:
τ_k = \frac {M_k} {W_k} = \frac {M_k} {π/16 * \frac {D^4 - d^4} {D}} ≤ τ_{DK}
D
d
vnější průměr hřídele
vnitřní průměr hřídele
Tvarové hřídele
Pokud jsou na hřídeli drážky, zápichy, osazení, je nutné zavést vrubový součinitel β, protože tyto vruby zvyšují napětí v krutu na povrchu hřídele.
Vliv vrubů omezíme:
- Zvýšením meze únavy povrchu materiálu např. cementováním, zušlechťováním, válečkováním, nitridováním nebo povrchovým kalením
- Konstrukční úpravou – vytvořením rádiusů.
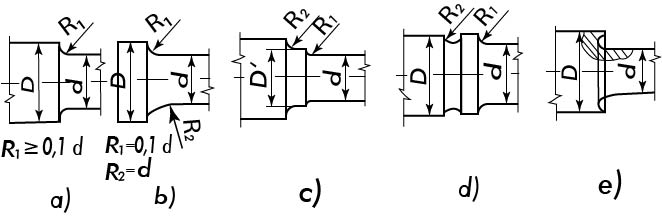
Obr. 14 Konstrukční úpravy v místě osazení
a) zaoblení poloměrem; b), c) pro větší změny průměrů – dva poloměry; d), e) význačné zmenšení vrubového účinku
Kritické otáčky hřídele
V důsledku nevyváženosti hmot dochází při rotaci hřídele ke vzniku odstředivých sil, které způsobují jeho průhyb.
Při určitých (kritických) otáčkách dochází k velkému průhybu, který může způsobit i porušení hřídele. Je to způsobeno tím, že se otáčky shodují s kmitočtem vlastního kmitání hřídele, dojde k rezonanci a výchylka teoreticky jde do nekonečna. Toto namáhání nemůže vydržet ani správně pevnostně dimenzovaný hřídel. Ve skutečnosti k tomu nedojde – útlum chvění vlivem materiálu hřídele, ložiska atd. Je proto důležité znát hodnotu kritických otáček (výpočtem), a pak zvolit provozní otáčky nižší nebo vyšší než kritické. Oblast kritických otáček, ve kterých hřídel nesmí pracovat, je (0,8 až 1,2) násobek nKR.
Drážkové hřídele (spoje)
Drážkový hřídel má po obvodu provedeny (vyfrézovány) podélné drážky, v podstatě pera. V náboji je stejný počet drážek. Drážkový hřídel tedy plní stejnou funkci jako perový spoj. Používá se především v případě, kdy je potřeba zajistit možnost axiálního posuvu rotačních součástí upevněných na hřídeli (nejčastěji ozubených kol). U pevných spojů je nutné zajištění proti axiálnímu posuvu upevněné součásti. Slouží pro přenos krouticího momentu – velká zatížení, střídavá a rázová.
Výroba je náročná na přesnost a nákladná, je třeba speciálního vybavení. Proto není drážkový spoj vhodný pro kusovou výrobu. Je nutné zajistit souosost a kolmost hřídele s nábojem. Spolehlivost spoje je nepříznivě ovlivněna vrubovými účinky drážek (hrozí únavový lom). Montáž a demontáž spoje je snadná. Drážkování je normalizováno.
Druhy drážkových spojů
- S rovnobokým drážkováním – použití pro posuvné náboje, velké a střídavé krouticí momenty (např. přesuvné ozubené kolo v převodovce, lamely spojky….).

a)
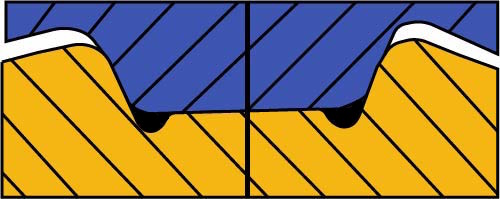
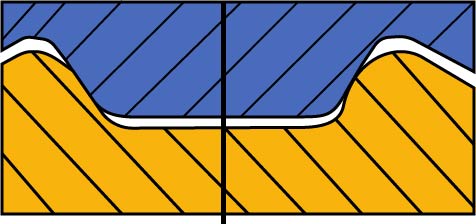
b) c) Obr. 15
a) Drážkový spoj s rovnobokým drážkováním; b) Vnitřní středění; c) Středění na boky drážek
- S jemným drážkováním – pro přenos velkých krouticích momentů, nevhodné pro přesuvné náboje, méně zeslabuje hřídel, zatěžující tlak je menší, náboj je na hřídeli možné přesadit o velmi malý úhel, použití pro uchycení torzních tyčí.

Obr. 16 Drážkový spoj s jemným drážkováním
- S evolventním drážkováním – pro přenos velkých a rázovitých krouticích momentů, náboj je možné přesadit o velmi malý úhel, použití – unášení lamel u lamelové spojky.

a)


b) c) Obr. 17
a) Drážkový spoj s evolventním drážkováním; b) Vnější středění; c) Středění na boky drážek
Výpočet délky drážkového spoje
- obvodová síla F a krouticí moment Mk jsou přenášeny tlakem boků zubů na hřídeli na boky drážek náboje a naopak.
Pevnostní rovnice – namáhání krutem
τ_k = \frac {M_k} {W_k} ≤ τ_{Dk}
W_k = π/16 * d^3 ≅ 1/5 * d^3, d_s = \frac {(D + d)} {2} [mm], M_k = F * {d_s}/{2}
Kontrolní výpočet – otlačení
p_D = \frac {F} {S' * l}
F = p_D * S' * l ⇒ l = \frac {F} {S' * p_D} = \frac {2M_k} {d_s * S' * p_D} [\text{mm}]
Při návrhu základních parametrů spoje je nutné dodržet podmínku, že délka náboje l nesmí být větší než 2d.
Použité veličiny:
S'
l
d_s
D
d
\text{p}_D
W_k
skutečná účinná plocha všech drážek na 1 mm délky náboje [\text{mm}^2] – Obr. Výběr
z normy ČSN 01 4942 – Drážková spojení rovnoboká, značeno A´
délka náboje [mm]
střední průměr náboje [mm]
velký průměr náboje [mm]
malý průměr náboje [mm]
dovolený tlak v opěrné ploše drážek [MPa]
modul průřezu v krutu
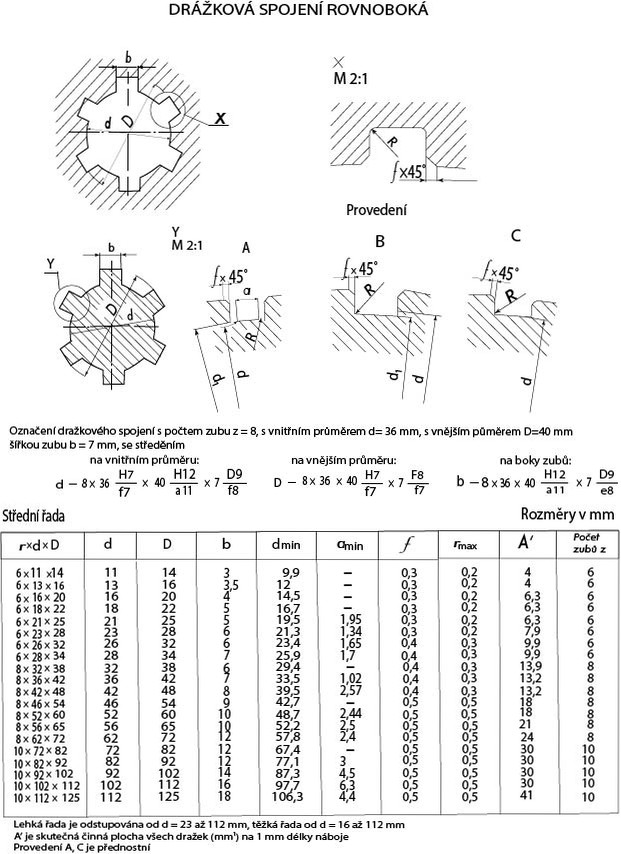
Obr. 18 Výběr z normy ČSN 01 4942 – Drážková spojení rovnoboká
Testové otázky
Použitá literatura:
R. Kříž a kol. Stavba a Provoz strojů strojů I. SNTL – Nakladatelství technické literatury. 1977