Obsah kapitoly
- 1.
Spoje a spojovací součásti
-
1.1
Rozebíratelné spoje
- 1.1.1 Šroubové spoje
- 1.1.2 Kolíkové spoje
- 1.1.3
Čepové spoje
- 1.1.3.1 Pevnostní výpočet čepového spoje
- 1.1.4 Klínové spoje
-
1.1.5
Perové spoje
- 1.1.5.1 Pevnostní výpočet perového spoje
- 1.1.6 Svěrné spoje
- 1.1.7 Pevnostní výpočet korýtkové spojky
-
1.1
Rozebíratelné spoje
- Testové otázky
1 Spoje a spojovací součásti
Dělení spojů podle principu působení spoje:
- Spoj s tvarovým stykem
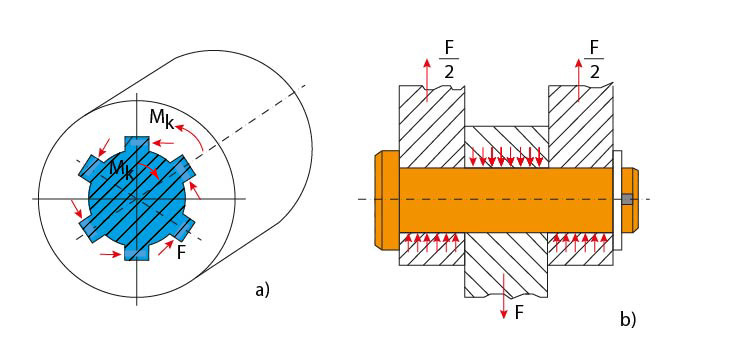
Obr. 1 Spoj s tvarovým stykem
- přenos krouticího momentu pomocí drážkového hřídele na drážkový náboj
- přenos síly normálovým napětím u kloubového spoje táhla s vidlicí pomocí čepu
Při tomto typu spoje dochází k přenosu sil mezi spojovanými částmi jen normálovým napětím nebo normálovými silami (tlak) mezi stykovými plochami.
- Spoje se silovým stykem
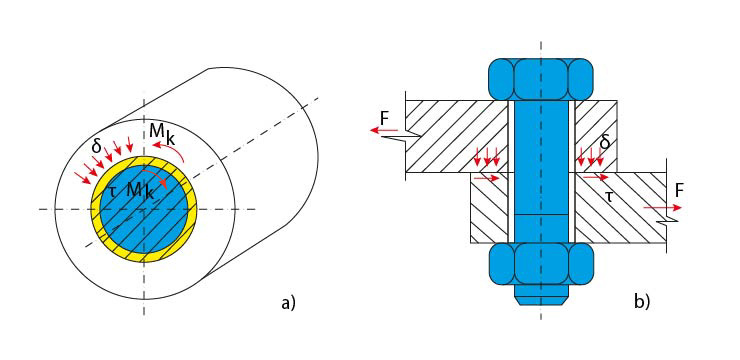
Obr. 2 Spoj se silovým stykem
- tlakový spoj hřídele s nábojem přenášející krouticí moment silovým stykem vzniklým předpětím tlakového spoje
- spoj volně průchozím šroubem, zatíženým silou kolmo k ose
Při tomto druhu spojení dochází ke spoji součásti vzepřením. Síly se přenášejí třením vyvolaným rozpěrnými normálovými silami podle Coulombova zákona.
- Spoj s materiálovým stykem
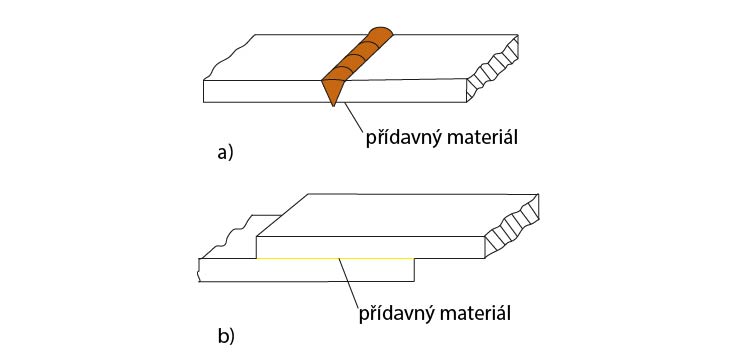
Obr. 3 Spojení materiálovým stykem
- přídavný materiál stejného charakteru a pevnosti jako základní materiál –svařování
- přídavný materiál jiného charakteru a menší pevnosti než základní materiál (materiál spojovaných součástí), tmelení, lepení, pájení
Při spojení materiálovým stykem dochází k vytvoření nerozebíratelného celku pomocí přídavného materiálu (svařování, lepení, pájení). V některých případech dochází ke kombinaci silového a tvarového styku, např. u šroubového spoje se někdy jedná o spoj silový, jindy tvarový. Klínové spoje jsou silové, ale k přenosu krouticího momentu u nich může docházet i tvarově. Nýtové spoje přenáší dané zatížení tvarově (tlakem), ale i silově (třením mezi spojovanými součástmi). Podrobně rozdělení spojů je uvedeno v tab. 1.
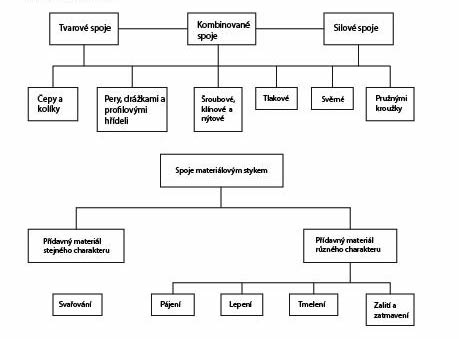
Tab. 1 Rozdělení spojů
Dělení spojů podle způsobu rozebírání spoje:
- Rozebíratelný spoj – spoj je možné vícekrát bez porušení rozebrat a znovu smontovat stejnými spojovacími součástmi (rozebíratelnost je omezená).
- Nerozebíratelný spoj – spoj nelze rozebrat bez destrukce spojovacích součástí.
Zpět na začátek
1.1 Rozebíratelné spoje
1.1.1 Šroubové spoje
Šrouby tvoří tvarový spoj – síla se z jedné součásti do druhé přenáší tvarovou spojovací součástí (šroubem). Někdy ovšem tvoří spoj silový – utažením šroubu před zatížením se vyvolá osová (normálová) síla předpětím šroubu i spojovaných součástí a tím i tření ve spoji. Vzniká tvarový spoj s předpětím, což je v podstatě silový spoj.
Základní druhy šroubových spojů:
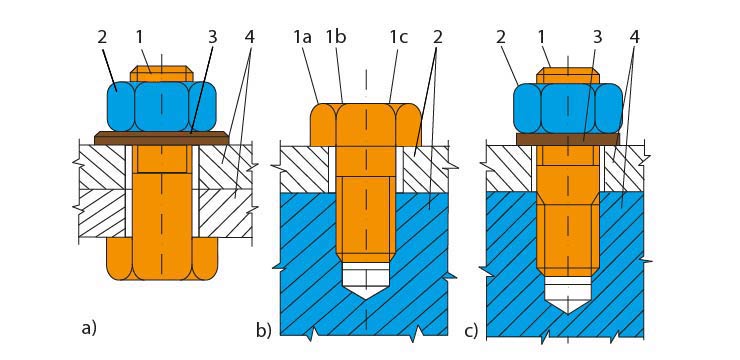
Obr. 4 Základní druhy šroubových spojů
- Spoj šroubem s hlavou a maticí – šroub je v díře uložen s vůlí: 1 – šroub s hlavou,
2 – matice, 3 – podložka, 4 – spojované součásti
- Spoj zašroubovaným šroubem s hlavou – šroub zašroubován ve spodní součásti, horní prochází s vůlí: 1 – šroub s hlavou, 2 – spojované součásti
- Spoj závrtným šroubem a maticí – šroub je zašroubován do spodní součásti až po konec výběhu závitu, horní součást, kterou šroub prochází s vůlí, se nasadí na šroub a přitáhne maticí. Při demontáži není nutné šroub vyšroubovat 1 – závrtný šroub, 2 – matice, 3 – pružná podložka, 4 – spojované součásti
Druhy šroubů, matic a podložek
Viz STAB.
Pojištění šroubových spojů
Při silném dotažení šroubového spoje mohou vzniknout plastické (trvalé) deformace na součástech tvořících spoj. Tyto se dále během provozu mohou prohlubovat (otlačení stykových ploch) a hrozí uvolnění spoje. Uvolnění spoje dále může být způsobeno i otřesy a jeho dynamickým namáháním (např. u automobilu).
V těchto případech je tedy nutné šroubový spoj pojistit:
- proti uvolnění – materiálovým stykem nebo použitím silových (třecích) či tvarových pojistek
- proti ztrátě matice (resp. šroubu) – pomocí tvarových pojistek
Příklady pojištění šroubových spojů:
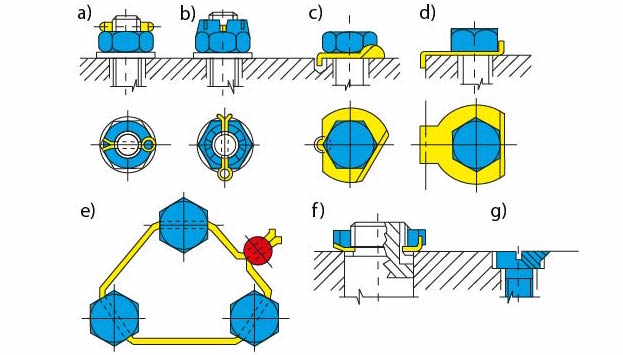
- závlačkou,
- korunovou maticí a závlačkou,
- pojistnou podložkou s nosem,
- pojistnou podložkou s jazýčkem,
- pojištění pomocí drátu a plomby (olověné nebo plastové),
- pojištění hřídelové matice KM pojistnou podložkou MB,
- pojištění zásekem okraje hlavy šroubu do spojovaného materiálu.
Obr. 5 Tvarové pojištění šroubů
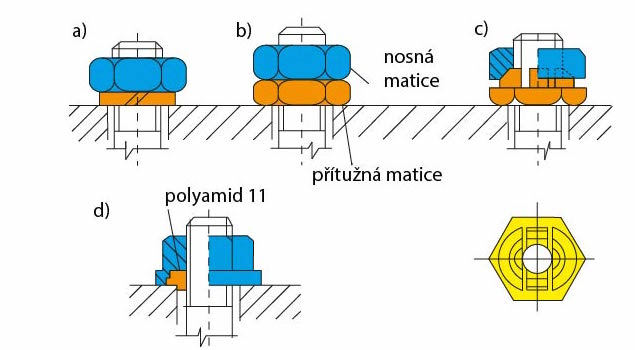
- pružnou podložkou,
- přítužnou maticí,
- pojistnou dvoudílnou maticí (na obrázku je v půdorysu nakreslena jen spodní část matice),
- těsnicí a pojistnou maticí Seal-Lock s připojeným tuhým kroužkem z polyamidu 11 uvnitř na dosedací straně.
Obr. 6 Silová pojištění šroubů
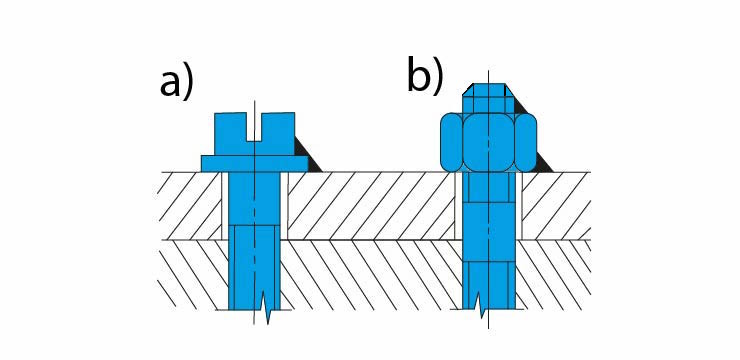
Obr. 7 Pojištění šroubů materiálovým stykem
a), b) přivařením, zakápnutím lakem nebo připájením – u malých šroubů lze hlavu a matici šroubu ke spojovanému materiálu i přilepit
Druhy závitů
Závit je šroubovitě vinutá drážka daného profilu (řez rovinou procházející osou šroubu nebo matice) tzn., každý bod opisuje šroubovici.
Dělení závitů:
- podle plochy, na které je závit vyroben – vnější (šrouby), vnitřní (matice)
- podle směru stoupání (podle vinutí) – pravé (pohyb ve směru smyslu pohybu hodinových ručiček), levé
- podle tvaru dříku – válcové, kuželové
- podle tvaru profilu – trojúhelníkové (metrický, palcový), lichoběžníkové, oblé
- podle počtu chodů – jednochodé (samosvorné, na dříku je vyřezána jedna šroubová drážka), dvouchodé, vícechodé
- podle účelu – spojovací (metrický, palcový, oblý), pohybové (lichoběžníkový – zvláštní)
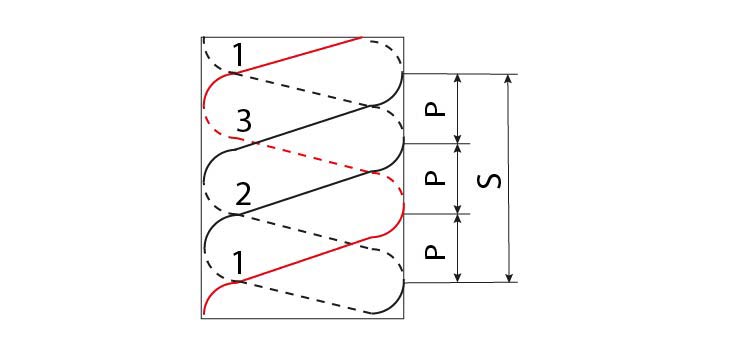
Obr. 8 Tříchodový závit
s – stoupání závitu, n – počet chodů závitu, P – rozteč
s = n x P
Značení závitů:
Metrický – nejpoužívanější, profil tvořen rovnostranným trojúhelníkem – 60°
- s hrubou roztečí: M d, např. M 24, d-velký průměr závitu,
- s jemnou roztečí: M d x P, M 24x2, levý M d x P LH, M 24 x 2 LH.
Palcový
- trubkový – použití pro spojení trubek ve vodovodních a plynových rozvodech, profil rovnoramenného trojúhelníku s vrcholovým úhlem 55°, rozměr D je světlost trubky (přibližná velikost vnitřního průměru trubky); stoupání je udáno počtem roztečí na 1palec (25,4 mm).
- válcový: G d“, G ¾‘‘
- kuželový: KG d“
- whitworthův – profil rovnoramenného trojúhelníku s vrcholovým úhlem 55°, v Evropě se používá výjimečně (jako stativové závity pro měřicí přístroje, fotoaparáty, kamery apod.).
- W d‘‘, W ½‘‘ (25,4/2) – rozměr d je velký ø závitu šroubu; stoupání je udáno počtem roztečí na 1 palec (25,4 mm)
Oblý
- profil složen z kruhových oblouků
- vhodný pro šrouby, které jsou vystaveny nárazům, prašnému prostředí a povětrnostním vlivům (např. u spojek železničních vozů)
- Rd d, Rd 32, kde d (druhé) je velký průměr závitu
Pozn.:
Zvláštní – Edisonův závit je závit se zaoblením, tvarem podobný oblému, ale s menším stoupáním. Značí se velkým písmenem E, za nímž následuje číslovka udávající průměr v mm. Edison jím roku 1881 vybavil žárovku. Závit patří mezi standardizované závity.
Lichoběžníkový rovnoramenný – vrcholový úhel 30°, osová síla může působit v obou směrech
- jednochodý: Tr d x S, Tr 48 x 8 – d je velký průměr závitu šroubu, S stoupání v mm.
- vícechodý: Tr d x S (P), Tr50 x 16 (P8)…dvouchodý, P rozteč, S stoupání.
Lichoběžníkový nerovnoramenný – tam, kde tlaková síla působí v jednom smyslu, např. u vřetenových lisů.
- S d x S, S 70 x 10
Zpět na začátek
1.1.1.1 Pevnostní výpočty šroubů
U dynamicky zatížených šroubů dochází k porušení nejčastěji v prvním zatíženém závitu. Z toho důvodu je vhodné zatížení rozložit na více závitů, např. tažnou maticí. Dalšími nebezpečnými místy jsou pro šroub výběh závitu a přechod dříku do hlavy. Porušení v těchto místech lze eliminovat vytvořením většího zaoblení (0,1d).
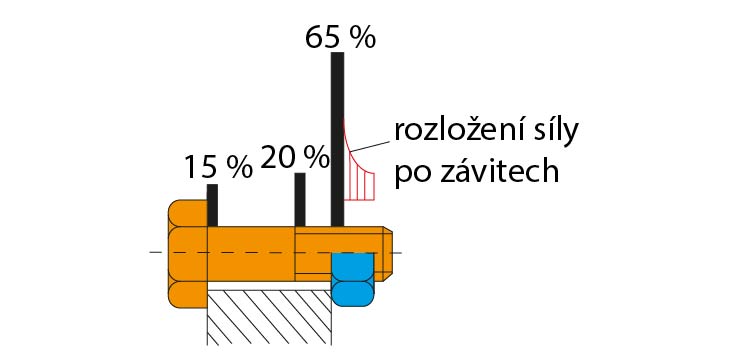
Obr. 9 Rozložení četnosti lomů normalizovaných šroubů při míjivém zatížení
65 % lomů – první zatížený závit
20 % lomů – výběh závitů
15 % lomů – pod hlavou šroubu
Rozdělení šroubových spojů podle způsobu zatížení a namáhání
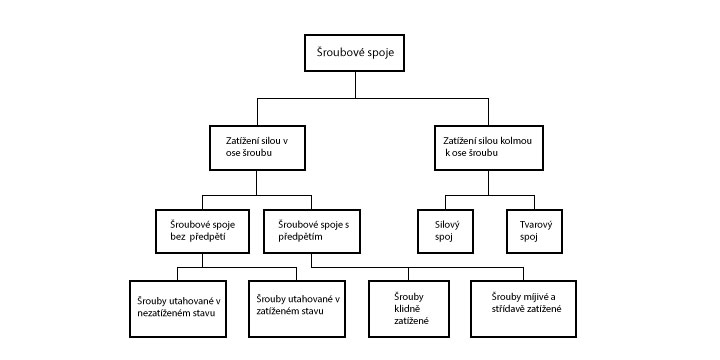
Tab. 2 Rozdělení šroubových spojů podle způsobu zatížení a namáhání
- Šrouby zatížené v ose – montované v nezatíženém stavu – jeřábový hák
- Šrouby zatížené v ose – montované v zatíženém stavu – výpočet šroubového napínače.
Příkladem je napínací šroub mezi napnutými táhly nebo lany. Šroub je silou F namáhán tahem a utahovacím momentem Mu v závitech při utahování. Pro správné dimenzování šroubu je zásadní výsledné namáhání (tah + krut), tzv. redukované napětí:
σ_{RED} = \sqrt {σ_t^2 + 3 * τ_k^2} ≤ σ_D
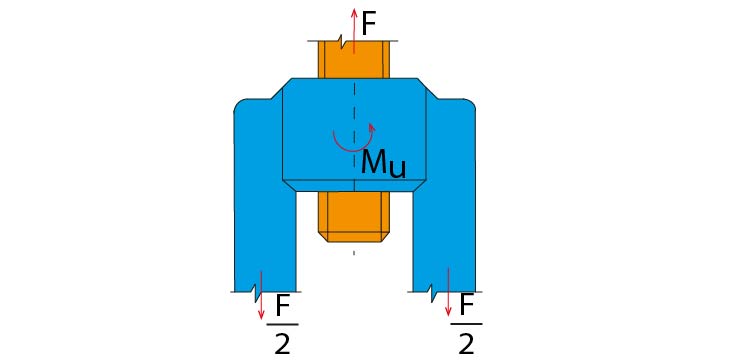
Obr. 11 Napínací šroub
Pevnostní rovnice:
Tah:σ_t = F/S ≤ σ_{D,t} [MPa]
Nebezpečný průřez:
S = \frac {πd_3^2} {4} [mm2]
Krut:
τ_k = \frac {M_k} {W_k} ≤ τ_{Dk} [MPa]
Modul průřezu v krutu:
W_k = π/16 * d_3^3 ≅ 1/5 d_3^3
Utahovací moment:
M_U = M_k = k * F_u * d/2
V praxi většinou není známa velikost utahovacího momentu MU, proto se používá zjednodušené rovnice:
σ_{RED} = σ_{t}/{0,75} ≤ σ_{D,t} \text{[MPa]}, σ_{t} = 0,75 * σ_{D,t}
Pak:
σ_{t} = 0,75 * σ_{D,t} = F/S ⇒ S = F/{0,75 * σ_{D,t}}
Je tedy zřejmé, že výpočet je stejný jako v případě šroubu zatíženého v ose, montovaného v nezatíženém stavu, jen se dovolená hodnota napětí σD,t sníží na 75 %.
- Spoje zatížené silou kolmou k ose šroubu
Spoje s tvarovým stykem – lícované šrouby
- jsou namáhány na smyk a otlačení- funkci kolíku (ustavení součásti, zajištění polohy)
- funkci šroubu (spojovací)
- Spoje se silovým stykem – např. přišroubování válcového profilu k desce pomocí vysoce předepjatých šroubů.
- Šrouby s předpětím – konstrukce diagramu předepjatého šroubu.
Jedná se o většinu šroubových spojů, zejména přírubové spoje a spoje u strojů pracujících s přetlakem.
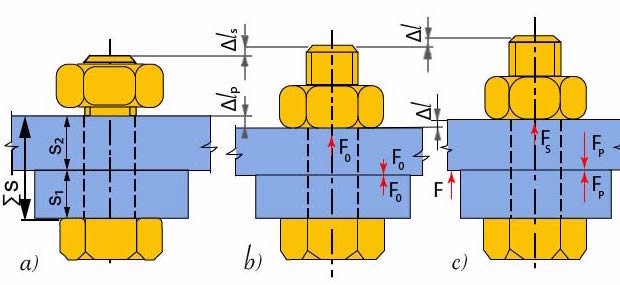
- spojení nepředepjato
- spojení předepjato nezatíženo
- spojení předepjato zatíženo provozní silou
Obr. 14 Síly a deformace ve šroubovém spoji
Pokud utahujeme šroub s předpětím na sílu FO, prodlouží se dřík o ∆ls. Zároveň se sevřené součásti (příruba včetně těsnění) zkrátí (stlačí) o ∆lp. Při následném působení provozní síly F se šrouby zatíží na sílu FS (maximální síla v ose šroubu) a sevřené součásti se odlehčí na sílu FP (zbytková síla – minimální síla při zatížení předepjatého spoje provozní silou). Pokud pomine působení síly F, soustava se vrátí do původního stavu, tzn. na šroub i přírubu působí síla FO.
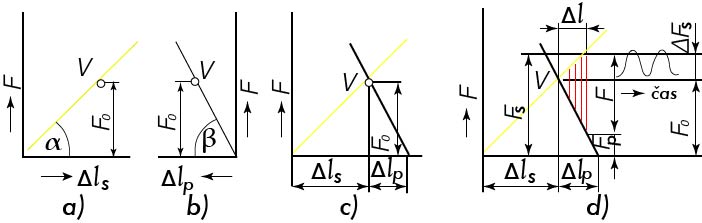
- charakteristika šroubu v diagramu F-∆l (síla – prodloužení)
- charakteristika přírub a těsnění v diagramu F-∆l
- diagram předpětí přírubového spoje při působení síly předpětí FO
- diagram předpětí přírubového spoje při působení provozní síly F při klidném zatížení, pokud je zatížení míjivé, síla F v závislosti na čase kolísá mezi FS a FO (v rozmezí ∆F)
Obr. 15 Postup konstrukce diagramu předepjatého spoje pro spojení přírub nebo desek (obr. 14)
FO – síla předpětí, F – provozní síla, FS – maximální síla ve šroubu, Fp – minimální (zbytková) síla předpětí spoje při zatížení provozní silou F
Dále k Obr. 15
- diagram prodloužení dříku
- diagram stlačení příruby včetně těsnění
- diagram předpětí přírubového spoje při působení síly předpětí
- diagram předpětí přírubového spoje při působení provozní síly při klidném zatížení/při míjivém zatížení
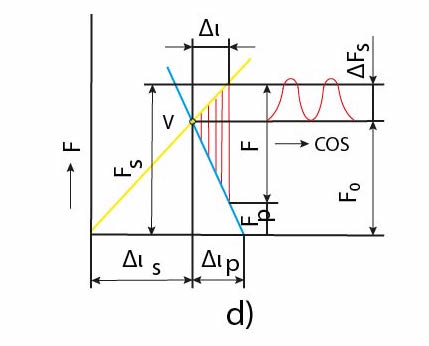
Obr. 16
Změna prodloužení dříku šroubu při působení provozní síly:
Δl'_S = Δl_S + Δl
Změna zkrácení příruby při působení provozní síly:
Δl'_P = Δl_P - Δl
\text{F}_O
\text{F}_S
F
\text{ΔF}_s
\text{F}_Psíla předpětí
maximální síla v ose šroubu
provozní síla
změna maximální síly v ose šroubu způsobená působením provozní síly
zbytková (minimální) síla při zatížení předepjatého spoje provozní silou
Při míjivém zatížení kolísá síla F mezi hodnotami FO a FS tzn. v rozmezí ∆FS.
Podmínkou funkčnosti spoje je:F_P > O
Pokud by došlo k situaci, že FP by byla menší nebo rovna nule, spoj se uvolní.
Montáž šroubu s předpětím:
- použití u ojnic, hlav spalovacích motorů, tlakových nádob atd. Jsou namáhány statickou nebo proměnlivou provozní silou.
- Dotažením klíče o předepsaný úhel – ze stoupání závitu a potřebného předpětí udaného silou FO se vypočte potřebný úhel pootočení, následně se z Hookova zákona vypočte velikost deformace dříku ∆l odpovídající úhlu pootočení (utažení) šroubu/matice.
- Mezním momentovým klíčem:
- torzní
- ohybový
- s pružinou
- se světelnou signalizací
- hydraulický
- se střižným kolíkem
- Měřením prodloužení dříku při utahování – číselníkovým úchylkoměrem nebo mikrometrickým hloubkoměrem.
- Elektrickým ohřevem šroubu při montáži – po zchladnutí na teplotu okolí se dřík smrští a vznikne předpětí.
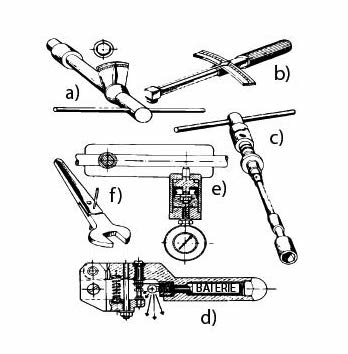
Obr. 17 Mezní momentové klíče
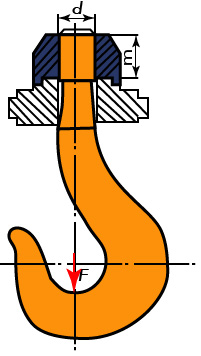
Obr. 10 Jeřábový hák
Šroub je namáhán provozní silou (u háku tíhou břemene) F na tah. Dále se kontroluje tlak na závity matice a šroubu, anebo se z dovoleného tlaku vypočte výška matice. U normalizovaných matic není třeba počítat jejich výšku a kontrolovat tlak v závitech matice.
Výpočet háku:
Pevnostní rovnice (tah):
σ_t = F/S ≤ σ_{D, t} [MPa]
Nebezpečný průřez S (nejužší místo na šroubu, malý průměr závitu \text {d}_3:
S = \frac {πd_3^2} 4 [mm2]
Výpočet potřebného malého průměru závitu \text {d}_3:
σ_{D, t} = F/S = \frac {4 * F} {πd_3^2} ⇒ d_3 = \sqrt \frac{4F} {σ_{D, t} * π} [mm]
Ve strojírenských tabulkách (STAB) vybereme vyhovující závit.
Výpočet výšky matice:
Pevnostní rovnice (tlak na závity matice a šroubu):
p = F/{S'} ≤ p_D [MPa]
Styková plocha závitu matice a šroubu, ve které hrozí otlačení:
S' = π * d_2 * H_1 * n [mm2]
Výpočet potřebného počtu závitů matice n:
p_D = \frac {F} {π * d_2 * H_1 * n} ⇒ n = \frac {F} {π * d_2 * H_1 * p_D}
Výpočet výšky matice m:
m = n * s
\text{d}_2 [mm]
\text{H}_1 [mm]
n
s
\text{p}_d [MPa]
\text{σ}_{D,t} [MPa]
střední průměr závitu (STAB)
nosná hlouba závitu (STAB)
počet závitů
stoupání závitu (STAB)
dovolený tlak (STAB)
dovolené napětí v tahu (STAB)
Příklad 1:
Vypočtěte potřebné minimální rozměry metrického závitu háku a výšku litinové matice z litiny 42 2420. Závěsný hák z oceli 11 600 je určen pro jmenovité zatížení F = 100 kN. Matice háku bude našroubována bez předpětí. Uvažujeme míjivé zatížení.
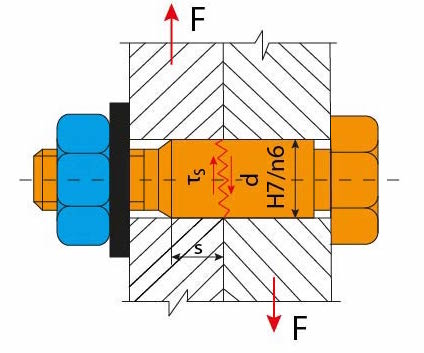
Obr. 12 Přenos síly kolmo k ose šroubu lícovaným šroubem
Pevnostní (návrhový výpočet) – smyk:
τ_S = F/S ≤ τ_{D ,S} [\text{MPa}]
Nebezpečný průřez dříku šroubu S:
S = \frac {πd^2} {4} [ \text{mm}^2]
Výpočet potřebného průměru dříku šroubu d:
τ_{D, S} = F/S = \frac {4 * F} {πd^2} ⇒ d= \sqrt \frac{4 * F} {τ_{D, S} * π} [\text{mm}]
Kontrolní výpočet: otlačení
Pevnostní rovnice:
p = F/{S'} ≤ p_D [\text{MPa}]
S' = d * s_{min}
Smin
minimální tloušťka součásti ve styku s dříkem lícovaného šroubu
(v obrázku označeno s)
Pozn.:
Lícované šrouby plní dvě funkce:
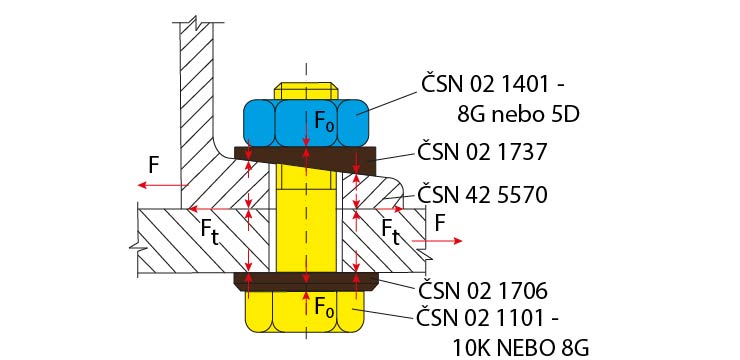
Obr. 13 Vysoce předepjaté šroubové spoje ve stavbě ocelových konstrukcí – připevnění nosníku U
Základní podmínka:
F ≤ F_t = F_o * f,
kde: Fo je síla předpětí šroubu vyvolaná jeho utažením
f je součinitel tření.
Zpět na začátek
1.1.2 Kolíkové spoje
Jedná se o nejjednodušší a nejstarší způsob spojení, jde o rozebíratelný spoj s tvarovým stykem. Kolíky jsou normalizované součásti sloužící k vytvoření pevného spoje dvou nebo více strojních součástí, k zajištění jejich přesné polohy a zachycení příčných posouvajících sil. Kolík je vsazen s předpětím, které je způsobeno buď přesahem naraženého kolíku vůči díře, nebo jeho kuželovitostí. Kuželové kolíky jsou samosvorné a mají kuželovitost 1:50.
Druhy kolíků
- Rozdělení dle tvaru:
- Válcové – jsou většinou lícované. Mohou být kalené, díry obvykle nutno stružit, vrtají a struží se současně ve všech spojovaných součástech. Pro snadnější montáž mají na koncích vyroben vodící kužel. Plní funkci zajišťovací, spojovací a vodicí.

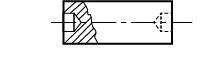
ČSN 02 21 50
Materiál: 11 107, 11 600
Kolík dosedací, zajišťovací a spojovací
Díru nutno vystružitČSN 02 21 52
Materiál: 19 421.4
Kolík zajišťovací, vodič, spojovací u nástrojů
Díru nutno vystružitČSN 02 2140
Materiál: 11 423, 42 405
Kolík k roznýtování, kloubový spoj
Bez vystruženíObr. 18 Příklady válcových kolíků
- Kuželové – většinou se používají jako spojovací. Kuželovitost 1:50 zajišťuje jejich samosvornost. Díry nutno současně ve všech spojovaných součástech kuželově vrtat a stružit. Pro demontáž ze slepých děr se používají kolíky se závitem (vnitřním nebo vnějším).
- Pružné – jsou kalené, v díře pruží. Díra se nestruží, kolík se přizpůsobí. Vhodný pro spoje vystavené vibracím a rázovým silám. Plní funkci zajišťovací a pojišťovací. Výhodou je úspora materiálu.
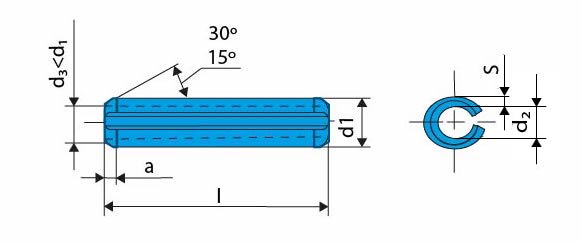
Obr. 21 Pružný kolík
- Rýhované – po obvodu mají tři rovnoměrně rozložené rýhy, jejich hloubka nemusí být po celé délce vždy stejná. Rýhy se po zaražení kolíku deformují a vyvolají radiální tlak, což zároveň zajišťuje kolík proti uvolnění. Díra se nestruží. Nevhodné pro použití u často rozebíraného spoje. Používají se jako spojovací, spojovací a pojišťovací nebo zajišťovací pro kloubový spoj.
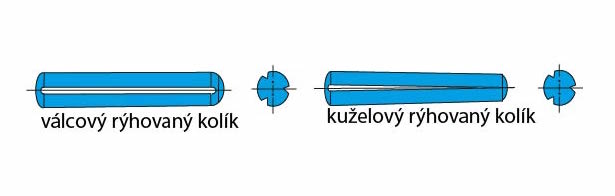
Obr. 22 Rýhované kolíky
- Hřeby – upevňovací hřeby, jejich použití je omezováno, např. pro samolepicí firemní a typové štítky, díra se nestruží.
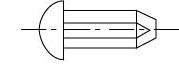
ČSN 02 2190
Materiál: 11 343
Rýhovaný hřeb upevňovací
Bez vystruženíČSN 02 2195
Materiál: 11 343.40
Šroubovaný hřeb upevňovací
Bez vystruženíObr. 23 Hřeby
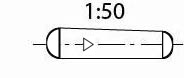
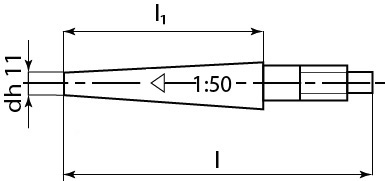
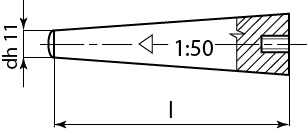
ČSN 02 21 53
Materiál: 11 107, 11 600
Kolík zajišťovací a spojovací
Díru nutno kuželově vystružitKuželové kolíky s vnějším závitem Kuželové kolíky s vnitřním závitem Obr. 19 Příklady kuželových kolíků
Obr. 20 Válcový (vlevo) a kuželový (vpravo) kolík
- Válcové – jsou většinou lícované. Mohou být kalené, díry obvykle nutno stružit, vrtají a struží se současně ve všech spojovaných součástech. Pro snadnější montáž mají na koncích vyroben vodící kužel. Plní funkci zajišťovací, spojovací a vodicí.
-
Rozdělení dle použití:
- spojovací a upevňovací – k pevnému spojení dvou součástí přenášejících krouticí moment, např. tyče na hřídeli
- unášecí – unášení jedné součásti druhou
- přídržné – přidržení součásti, např. pružiny
- střižné – brání proti přetížení, např. střižný kolík u pojistné spojky
- kloubové – kloubové a otočné spojení dvou součástí
- pojišťovací – proti posunutí nebo pootočení
- zajišťovací – zajištění vzájemné polohy, např. dvou polovin převodové skříně
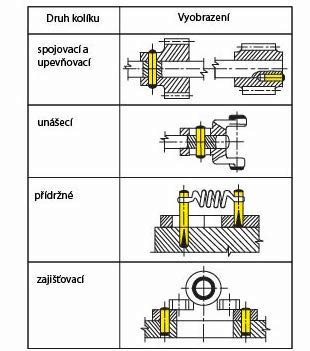
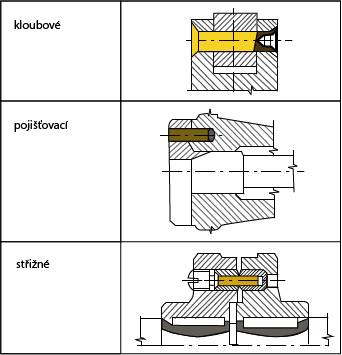
Obr. 24 Druhy kolíků dle použití
Zpět na začátek
1.1.2.1 Pevnostní výpočty kolíkových spojů
- Zajišťovací kolík
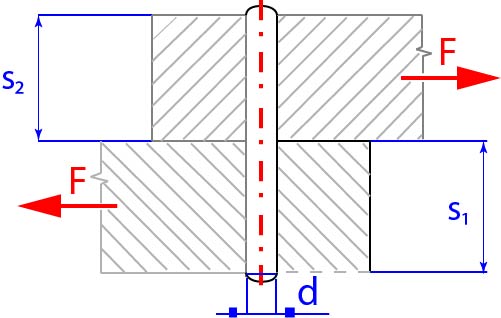
Obr. 25 Kolíkový spoj zajišťovacím kolíkem
Kolík je zatížen příčnou silou vyvolávající smyk kolíku. Je třeba provést pevnostní výpočet na smyk kolíku a otlačení stykových ploch.
Návrhový výpočet: smyk
Pevnostní rovnice:τ_S = F/S ≤ τ_{D,S} [\text{MPa}]
Nebezpečný průřez kolíku S:
S = {πd^2}/4 [\text{mm}^2]
Výpočet potřebného průměru kolíku d:
τ_{D,S} = F/S = \frac{4 * F} {π * d^2} ⇒ d = \sqrt \frac {4*F}{τ_{D,S} * π} [\text{mm}]
Kontrolní výpočet: otlačení
Pevnostní rovnice:p = F/{S'} ≤ p_D [\text{MPa}]
- s1 = s2 = s
- s1 ≠ s2 ⇒ smin
p_D = F/{S'} = F/{d * s} ⇒ d = F/{s *p_D} [\text{mm}]
V STAB vybere odpovídající druh kolíku o nejbližším vyšším průměru než je průměr navržený výpočtem.
Použité veličiny:
\text{τ}_{D,S}
\text{s}_1, \text{s}_2
\text{p}_D
d
Sdovolené napětí materiálu ve smyku [MPa]
tloušťky spojovaných materiálu [mm]
dovolený tlak [MPa]
průměr kolíku [mm]
nebezpečný průřez kolíku [mm2]
- Spojovací a upevňovací kolík – příčný kolík v táhle a objímce
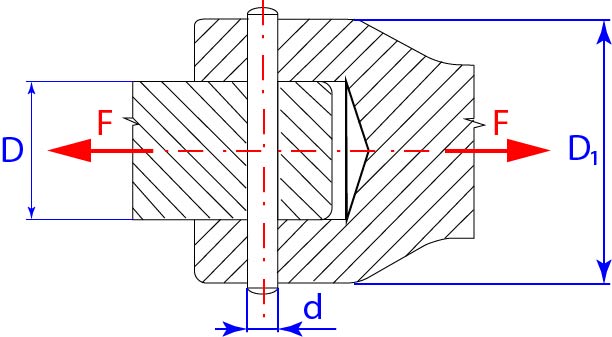
Obr. 26 Příčný kolík v táhle a objímce
Kolík je zatížen příčnou silou vyvolávající smyk kolíku. Je třeba provést pevnostní výpočet na smyk kolíku a otlačení stykových ploch.
Doporučené rozměry spoje:
d = (0,2 až 0,3) D
D1 = (1,5 až 2) D – pro náboj z oceli
D1 = 2,5 D – pro náboj z šedé litiny
Návrhový výpočet: smyk
Pevnostní rovnice:
τ_S = F/{2 * S} ≤ τ_{D,S} [\text{MPa}]
Nebezpečný průřez kolíku S:
S = {πd^2}/4 [\text{mm}^2]
τ_{D,S} = F/{2 * S} = \frac{2 * F} {π * d^2} ⇒ d = \sqrt \frac {2*F}{τ_{D,S} * π} [\text{mm}]
Kontrolní výpočet: otlačení
- tlak v táhle
p_1 = F/{S_1} = F/{D * d} ≤ p_D [\text{MPa}]
- tlak v objímce
p_2 = F/{S_2} = F/{d * (D_1 - D)} ≤ p_D [\text{MPa}]
Použité veličiny:
|
τD,S |
dovolené napětí materiálu ve smyku [MPa] |
|
S1, S2 |
nebezpečný průřez kolíku při otlačení v táhle/v objímce [mm2] |
|
pD |
dovolený tlak [MPa] |
|
d |
průměr kolíku [mm] |
|
S |
nebezpečný průřez kolíku [mm2] |
|
D |
průměr táhla [mm] |
|
D1 |
průměr objímky [mm] |
Zpět na začátek
1.1.3 Čepové spoje
- vytvoření rozebíratelného spoje s tvarovým stykem pomocí spojovacího čepu. Spojovací čepy jsou v podstatě tlusté válcové kolíky uložené v součástech s vůlí, vytvářející kloubové spojení (zajištění pák, lanových kotoučů, oběžných kol apod.). Mohou přenášet větší zatížení než kolíky. Mohou také nahrazovat krátké nosné hřídele pojezdových kol, kladek apod. – nutno mazat.
Čepové spoje jsou levné, montáž i demontáž spoje je snadná. Přenáší jen radiální zatížení, musí být axiálně zajištěny.
Materiál čepů je nejčastěji automatová ocel (11 107), dále pak ocel 11 500, 11 600, 12 020 pro čepy namáhané na otěr, 14 220.
Druhy spojovacích čepů
- hladké
- bez otvorů
- s otvor pro závlačku
- s hlavou
- bez otvorů
- s otvory pro závlačku
- se závitovým koncem
- duté
- pružné
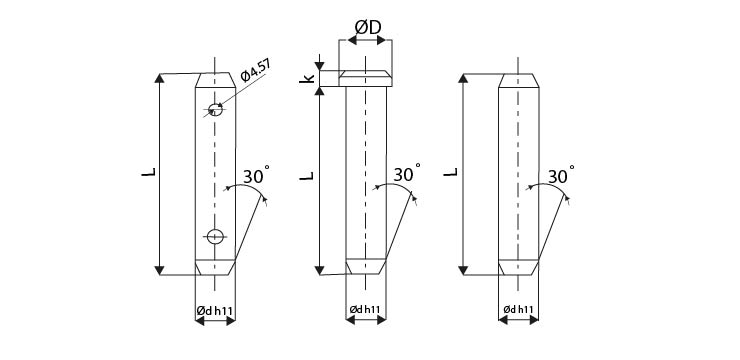
Obr. 27 Příklady spojovacích čepů
a) čep hladký, s otvory pro závlačku, b) čep s hlavou bez otvorů, c) čep hladký bez otvorů
Zajištění čepů
- proti posunutí a vypadnutí
- závlačkami a hladkou podložkou (Obr. 28 a)
- pojistnými třmenovými kroužky (Obr. 28 b)
- pojistnými pružnými hřídelovými kroužky (Seegerovy kroužky) (Obr. 28 c)
- maticí na závitovém konci čepu (Obr. 28 d)
- stavěcími kroužky se závlačkou nebo kuželovým kolíkem
- drátěnými pojistkami
- proti pootočení
- kolíky
- pojistnými kroužky
- přišroubováním přídržky (Obr. 28 e)
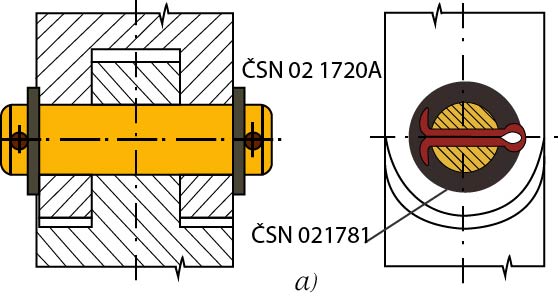
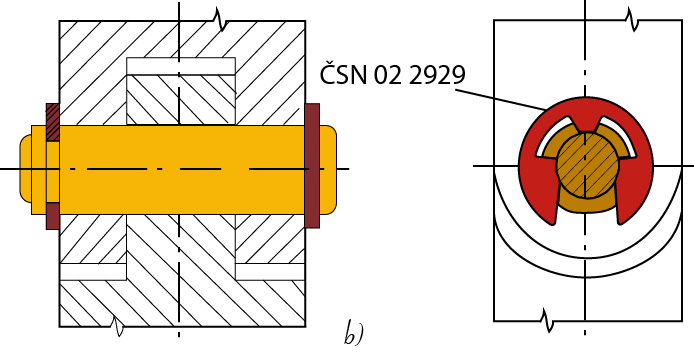
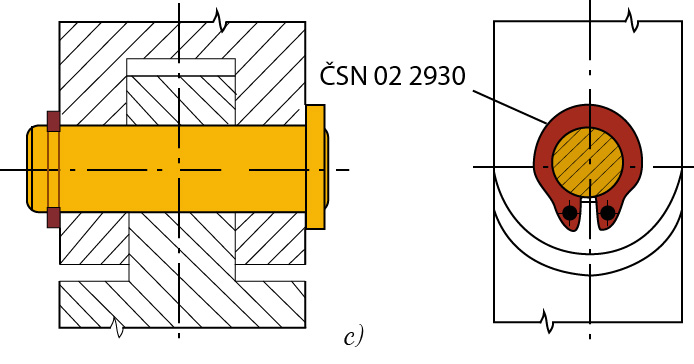
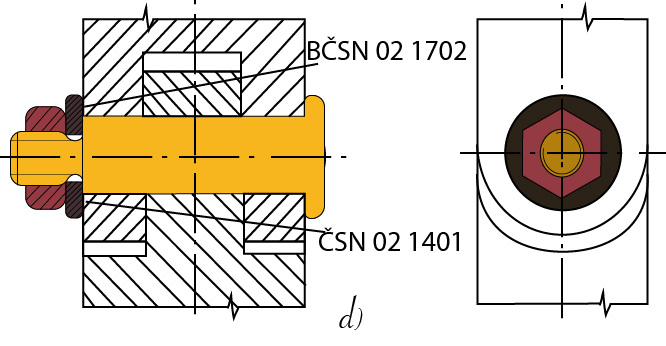
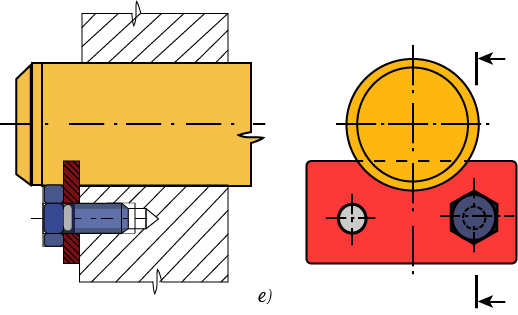
Obr. 28 Zajištění čepu proti posunutí a vypadnutí
Zpět na začátek
1.1.3.1 Pevnostní výpočet čepového spoje
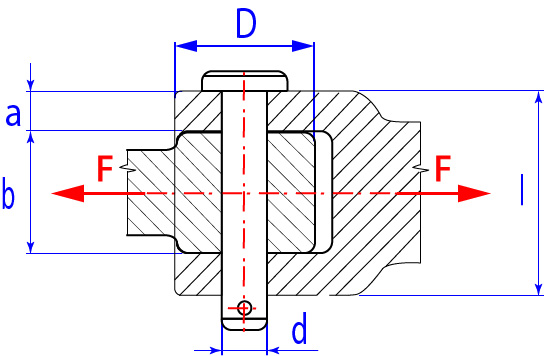
Obr. 29 Kloubové spojení táhla s vidlicí pomocí spojovacího čepu
Čep je zatížen příčnou silou na ohyb. Při dimenzování čepového spoje se provádí výpočet čepu na ohyb a otlačení stykových ploch, namáhání smykem se zanedbává. Při namáhání ohybem se o čepu uvažuje jako o nosníku uloženém na dvou podporách, zatížených spojitým břemenem rovným šířce táhla (síla F). Toto břemeno se poté nahrazuje dvěma osamělými silami (síla F/2).
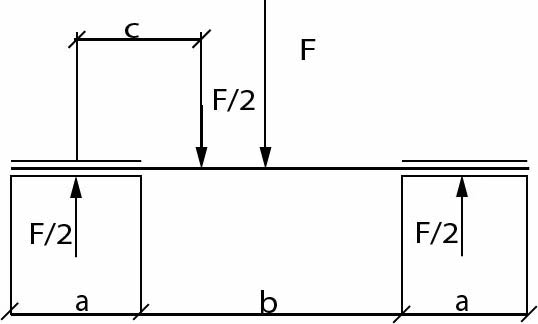
Návrhový výpočet: ohyb
Pevnostní rovnice:
σ_O = {M_{Omax}}/{W_O} ≤ σ_{DO} [\text{MPa}]
W_O = {πd^3}/32
Výpočet maximálního ohybového momentu Momax:
M_{Omax} = F/2 * c
c = a/2 + b/4 = {2a + b}/4
Pak:
M_{Omax} = F/2 * {2a + b}/4 = F/8 * (2a + b)
Výpočet potřebného průměru čepu d:
σ_{DO} = {M_{Omax}}/{W_O} ⇒ σ_{DO} = {32 * M_{Omax}}/{π*d^3} ⇒ d = \root 3 {\ frac {32 * M_{Omax}} {π * σ_{DO}}}
Kontrolní výpočet: otlačení
p = F/{S'} ≤ p_D
- tlak na vidlici
p_1 = \frac {F/2} {S'_1} = F/{2 * a * d} ≤ p_D [\text{MPa}]
- tlak v táhle
p_2 = \frac {F} {S'_2} = F/{b * d} ≤ p_D [\text{MPa}]
Zpět na začátek
1.1.4 Klínové spoje
Rozebíratelné spojení hřídele s nábojem s kombinovaným stykem. Jedná se o předepjatý spoj, kdy je krouticí moment přenášen převážně třením. U drážkových klínů částečně boky klínů a drážek. Naražením náboje na klín (vsazené klíny), anebo klínu mezi náboj a hřídel dojde k vzepření náboje o hřídel, tzn. v podstatě k nalisování klínu mezi hřídel a náboj. Klíny zajišťují náboj proti osovému posuvu.
Pro přenos střídavých Mk se používá dvou klínů přesazených o 120°.
Nevýhodou použití klínového spoje je nesouosost hřídele a náboje vedoucí k házení – nelze použít u převodů ozubenými koly. Pro eliminaci házení je třeba, aby vůle mezi hřídelem a nábojem byla minimální.
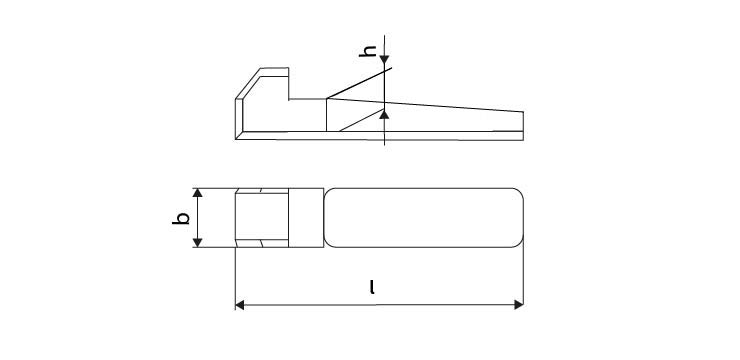
Obr. 30 Drážkový klín s nosem
Druhy klínů
- Spojovací klíny
- podélné – normalizované, osa klínu a spojované součásti jsou rovnoběžné
- příčné – osa klínu je kolmá na osu spojovaných součástí
- Stavěcí klíny – slouží k nastavení vzájemné polohy součástí
Podélné klíny – na jedné svojí straně mají úkos 1:100, v drážce je shodný úkos. Existují varianty s nosem a bez nosu.
Základní druhy:
- Třecí – Mk přenáší pouze třením, určen pro přenos malých momentů, vhodný pro dočasné spojení hřídel s nábojem. Tento spoj je určen pro přenos přibližně třetinového krouticího momentu určeného pro hřídel. Na hřídeli je vyrobena zaoblená plocha se stejným poloměrem, jaký má plocha na spodní straně klínu.
- Ploský – Mk přenáší převážně třením, určen pro přenos malých momentů. Na hřídeli je vyrobena dosedací plocha šířky b, na kterou se klín usadí. Je schopen přenést třetinu krouticího momentu, na který je dimenzován hřídel.
- Drážkový klín – vsazen do drážky v náboji, určen pro přenos větších krouticích momentů. Pokud je spoj umístěn ve střední části hřídele, drážka pro klín by měla mít alespoň dvojnásobnou délku než klín.
- Tangenciální (tečný klín) klín – jedná se o dva páry vzájemně přesazených klínů o 120°. Umožňují přenos velkých rázových Mk v obou směrech (vhodné pro naklínování setrvačníků). Nedochází k velkému zeslabení hřídele. Úkos není normalizován, pohybuje se v rozmezí 1:60 až 1:100.
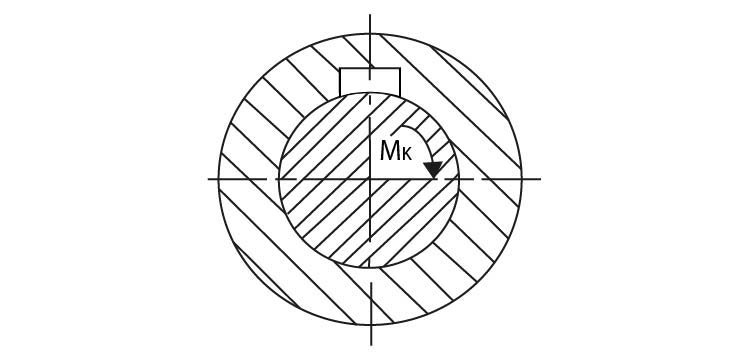
Obr. 31 Třecí klín
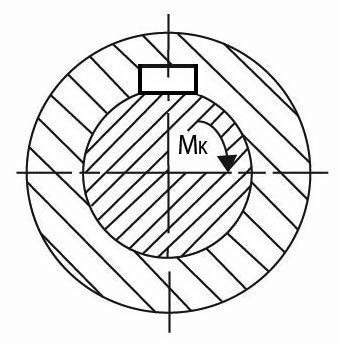
Obr. 32 Ploský klín
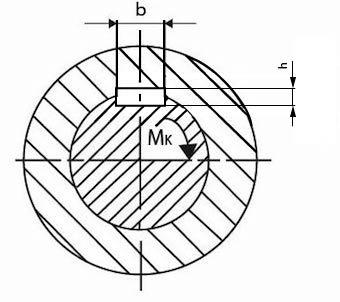
Obr. 33 Drážkový klín
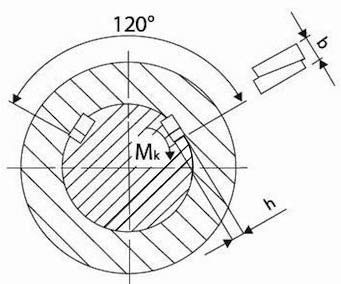
Obr. 34 Tangenciální klín
Velikost vhodného klínu volíme ze STAB na základě průměru hřídele. Návrhový a kontrolní výpočet klínů se obvykle neprovádí. Jen v případě použití velmi krátkého klínu je vhodné provést kontrolní výpočet na otlačení.
Zpět na začátek
1.1.5 Perové spoje
Pera slouží k přenosu krouticího momentu z hřídele na náboj a k zajištění axiální pohybu náboje po hřídeli. Spojují tedy hřídel s nábojem pomocí drážek, které se do náboje frézují, v náboji obrážejí. Jde o spoj s tvarovým stykem – silové zatížení je přenášeno bočními plochami pera.
Druhy per – rozdělení dle tvaru a funkce
- Těsná – funkční plochou jsou boky pera. Mezi dnem drážky v náboji a horní plochou pera je vůle. Pero je v drážce uloženo s přesahem.
- Výměnná – délka pera je větší než délka náboje. Zajišťuje axiální posuv náboje po hřídeli. Pero je v drážce uloženo s vůlí (nedojde tak ke vzniku tření při posuvu náboje po hřídeli), uchyceno je pomocí jednoho nebo dvou šroubů.
- Úsečová (Wooddruffova, kotoučová) – pro uložení krátkých nábojů. Vhodné v případě, kdy má drážka v náboji úkos. Tvar pera umožňuje jeho nastavení do vhodné polohy.
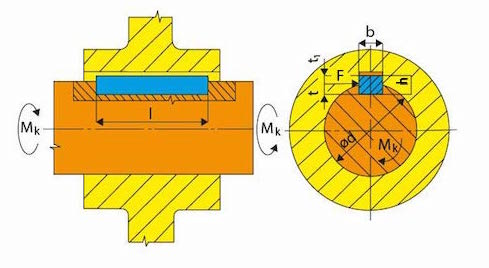
Obr. 35 Perový spoj – těsné pero
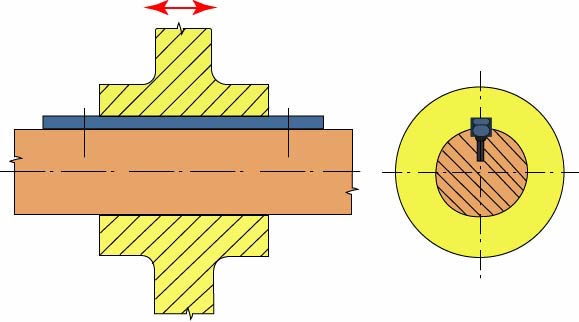
Obr. 36 Perový spoj – výměnné pero
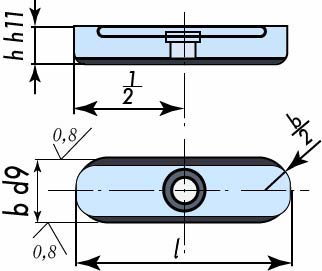
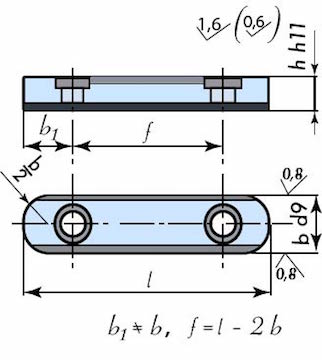
Obr. 37 Výměnná pera – uchycení jedním nebo dvěma šrouby
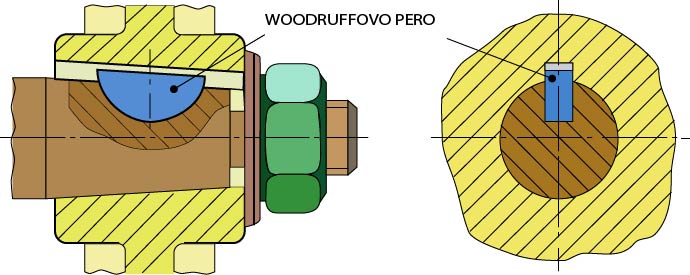
Obr. 38 Perový spoj – úsečové pero
Obr. 39 Úsečové pero a drážka pro úsečové pero v klikovém hřídeli
Obr. 40 Těsné (vlevo) a úsečové (vpravo) pero
Zpět na začátek
1.1.5.1 Pevnostní výpočet perového spoje
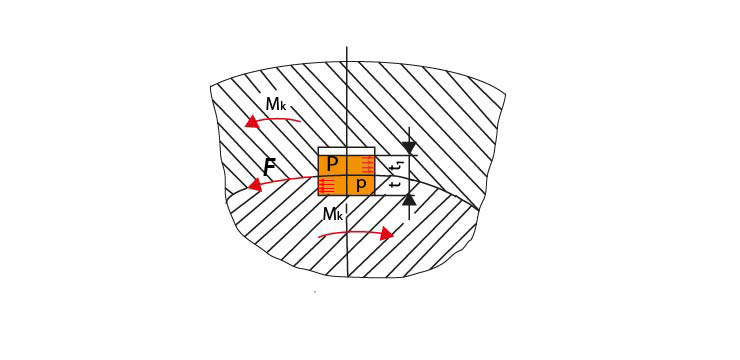
Obr. 41 Silové poměry u perového spoje
Při spojení perem tlačí boční stěny drážky na boční stěny per a naopak – jsou namáhány na otlačení. A dále pak na smyk. Pera se obvykle nepočítají z pevnostní rovnice, jsou normalizována a přiřazena k průměrům hřídele včetně úchylek a tolerancí. Norma určuje šířku a hloubku drážky a šířku a výšku pera. Je však třeba stanovit potřebnou délku pera.
Návrhový výpočet: otlačení
Pevnostní rovnice:
p = F/{S'} ≤ p_D
Stanovení obvodové síly F ze známého Mk:
M_k = F * d/2 ⇒ F = {2 * M_k}/{d} [N]
p_D = \frac {F} {t_1 * l} = \frac {2 * M_k} {t_1 * l * d} ⇒ l = \frac {2 * M_k} {t_1 * p_D * d} [\text{mm}]
Kontrolní výpočet: smyk
τ_S = F/S ≤ τ_{D,S} [\text{MPa}]
S = b * l [\text{mm}^2]
Použité veličiny:
\text{M}_k
d
l
\text{t}_1
\text{p}_D
b
krouticí moment [Nmm]
průměr hřídele [mm]
délka pera [mm]
hloubka drážky v náboji [mm]
dovolené otlačení (40 až 50 MPa pro náboj z šedé litiny, 90 až 100 MPa pro náboj z oceli)
šířka pera [mm]
Příklad 2:
Navrhněte pero pro vytvoření perového spoje hřídele s nábojem sloužící pro přenos krouticího momentu o velikosti M_k = 180 Nm. Průměr hřídele d = 40 mm, p_D = 90 MPa,
τ_{D,S} = 100 MPa.
Zpět na začátek
1.1.6 Svěrné spoje
Jedná se o rozebíratelné spoje se silovým stykem. Fungují tedy na principu tření ve stykových plochách, díky kterému dochází k pevnému spojení a přenosu silových zatížení z jedné součásti na druhou. Použití v případech, kdy je nutná častější změna polohy součásti. Náboj lze na hřídeli upevnit v libovolné poloze. Hřídel není zeslabena otvory, drážkami apod.
Druhy svěrných spojů
- Svěrný spoj se šroubem – např. spojení kliky s hřídelem.
- Svěrný spoj s kuželem - spojení rotačních částí na konci hřídele, např. hřídele s ozubeným kolem, řemenicí apod.
- Rozpěrný spoj s pružnými kroužky – spoj hřídele s nábojem v libovolném místě na hladké hřídeli, spoj je tvořen jedním až čtyřmi páry kuželových kroužků.
-
Další příklady svěrných spojů
- s celistvým nábojem a šroubem
- vzepřením vnitřní součásti
- s klínem
- plošný se šroubem
- s výstředníkem (excentrem)
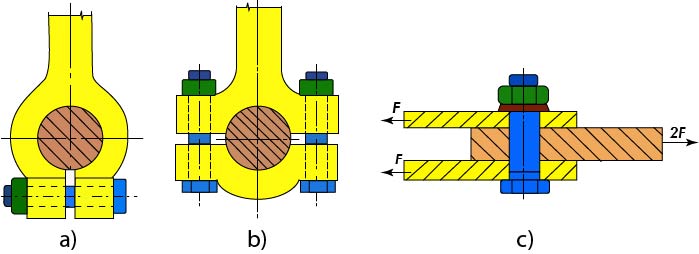
Obr. 42 Svěrný spoj se šroubem
a) s děleným nábojem, b) s rozříznutým nábojem, c) spojení plochých součástí
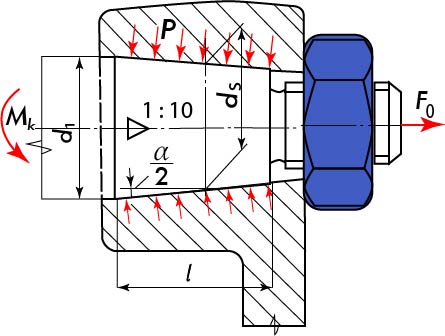
Obr. 43 Svěrný spoj kuželového konce hřídele s nábojem
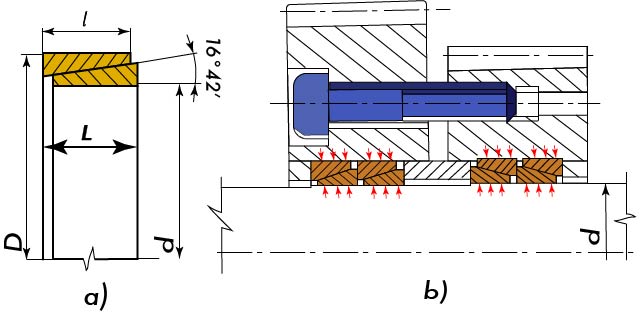
Obr. 44 Rozpěrný spoj s pružnými kroužky
a) Pár pružných kuželových kroužků, b) Upevnění ozubených kol na hladkém hřídeli pružnými kroužky a upínacími šrouby
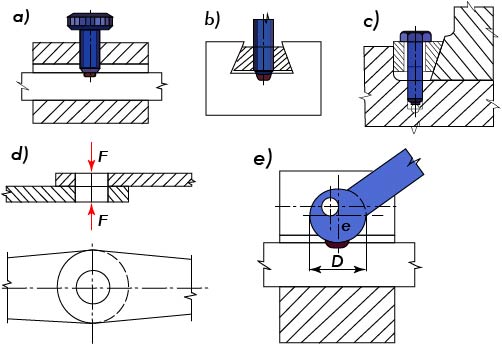
Obr. 45 Další příklady svěrných spojů
Zpět na začátek
1.1.7 Pevnostní výpočet korýtkové spojky
Odkaz na korýtkovou spojku z kapitoly Spojky.
Podmínkou přenosu krouticího momentu je:
M_k < M_{sv}
M_{sv} = k_s * M_k
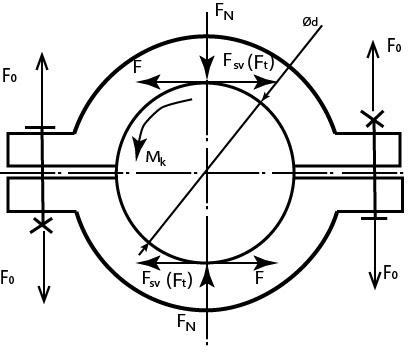
Obr. 46 Příklad korýtkové spojky
Výpočet potřebné síly předpětí ve šroubu FO:
M_{sv} = F_t * d = F_N * f_č * d = F_O * n * f_č * d
Pak:
M_{sv} = M_{sv}
F_O * n * f_č * d = k_s * M_k ⇒ F_O = \frac {k_s * M_k} {n * f_č * d} [N]
Použité veličiny:
\text{M}_k
d
\text{f}_č
n
\text{F}_O
F
\text{F}_{sv} (Ft)
přenášený krouticí moment [N.mm]
průměr hřídele [mm]
součinitel čepového tření (v STAB)
počet šroubů ve spojce
síla předpětí v jednom šroubu [N]
obvodová síla [N]
svěrná (třecí) síla [N]
F_{sv} = f_č * F_N
FN
normálová síla [N]
F_N = n * F_O
ks
součinitel bezpečnosti proti prokluzu, zpravidla rovno 1,8
Zpět na začátek
Testové otázky
Použitá literatura:
R. Kříž a kol. Stavba a Provoz strojů strojů I. SNTL – Nakladatelství technické literatury. 1977