- 1 Úvod do korelační analýzy
- 2 Závislost spojitých kvantitativních znaků - Pearsonův korelační koeficient
1 Úvod do korelační analýzy
Dvourozměrná náhodná veličina
Pro regresní analýzu je typické, že závisle proměnná závisí na nezávisle proměnné prostřednictvím nějaké funkční závislosti a náhodné veličiny, kterou používáme k vyjádření chyby měření. Závisle i nezávisle proměnná jsou jednorozměrné náhodné veličiny. Často taková jednosměrná závislost není vhodná k vystižení vztahů mezi veličinami.
V případě, že očekáváme mezi dvěma proměnnými lineární vztah a nemůžeme tvrdit, že jedna proměnná přímo ovlivňuje hodnoty druhé proměnné, použijeme k vyhodnocení vztahu korelační analýzu. Dosud jsme probírali jednorozměrnou náhodnou veličinu, která se dá nejvhodnějí popsat pomocí svojí hustoty. Znamená to, že pravděpodobnost, že náhodná veličina bude v intervalu < a; b > je rovna ploše pod křivkou hustoty od bodu a do bodu b.
Při korelaci sledujeme spíš společný vývoj obou proměnných. Proto mluvíme o dvourozměrné náhodné veličině. Pro popis dvourozměrné náhodné veličiny, tzn. výskytu různých dvojic čísel, použijeme plochu, které budeme také říkat hustota. Pravděpodobnost, že dvourozměrná náhodná veličina, tedy dvojice čísel, padne do nějaké dvourozměrné oblasti bude úměrná objemu pod plochou. Je to prostá analogie, jsme jen o rozměr výš.
Aby plocha mohla reprezentovat dvourozměrnou hustotu, musí mít vlastnosti, které na ni klade počet pravděpodobnosti. Především musí být plocha jako funkce dvou proměnných nezáporná, aby objemy mezi plochou a rovinou x,y byly nezáporné a mohly se interpretovat jako pravděpodobnosti. Aditivnost ověříme tak, že si uvědomíme aditivnost objemů. Jev jistý musí mít pravděpodobnost rovnu jedné, čili celkový objem pod hustotou musí být roven jedné. Tím jsou požadavky kladené na definici pravděpodobnosti splněny.
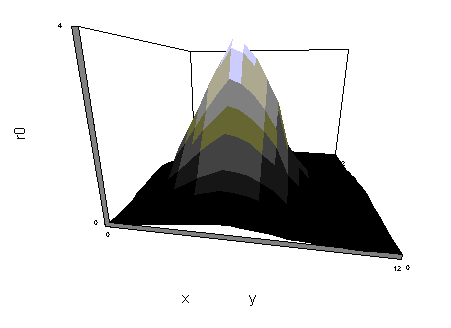
(Plochy je nejvhodnější zobrazovat pomocí vrstevnicových map. Mají totiž jen jednu potíž. Ta spočívá v tom, že se nedá rozpoznat, zda se jedná o plochu tvaru kráteru nebo o vrchol. Aby se toto odstranilo, je vždy vhodné před prohlížením vrstevnicové mapy plochy zkontrolovat perspektivní zobrazení plochy pomocí sítě. Představíme si, že na plochu je hozena síť. Při pohledu na tuto síť se pak snadno ujasní, kde jsou vrcholy a kde údolí i u složitějších ploch. Po pochopení tvaru plochy se už věnujeme jen vrstevnicové mapě.)
2 Závislost spojitých kvantitativních znaků - Pearsonův korelační koeficient
Korelační koeficient (r)
Účelem korelačního koeficientu je numericky popsat, zda se jedná o dvourozměrnou náhodnou veličinu, ve které jsou jednotlivé složky závislé či nezávislé.
Korelační koeficient r Є< -1;1 >. Tedy r = 0 znamená nezávislost. Jestliže se r blíží jedné nebo minus jedné, jedná se o silnou závislost. To je vidět také na následujících obrázcích. Na vrstevnicové mapě pro plochu při r = 0 vidíme, že vrstevnice mají tvar kruhu. Může to být také elipsa. Podstatná je symetrie jak vertikální, tak horizontální.
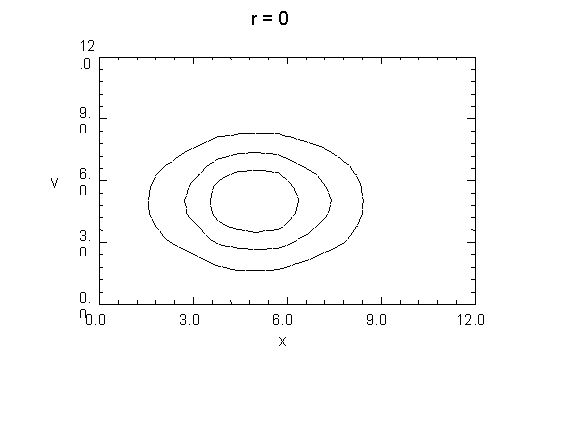
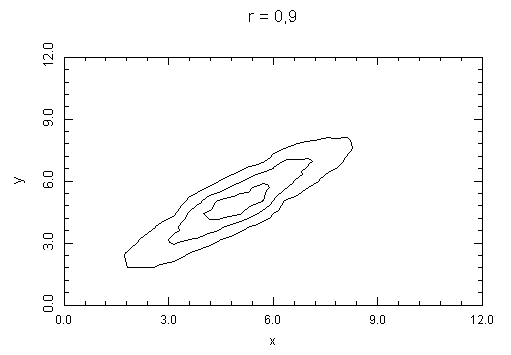
Druhá vrstevnicová mapa znázorňuje případ, kdy r = 0,9. Je jasně vidět, že osa symetrie dvourozměrné hustoty je skloněná. To je možné číst také tak, že si všímáme, kde je hustota nejvyšší. Z toho by bylo možné usoudit, že čím je větší x, tím je větší y. Je ale třeba to chápat spíš tak, že větší x a y nebo menší x a y nastanou s větší pravděpodobností než malá x a velká y nebo velká x a malá y. Nejedná se o kauzalitu, protože jde o dvourozměrnou náhodnou veličinu.

Objasnění výpočtu korelačního koeficientu
Základní popisná charakteristika, kterou se hodnotí závislost u dvourozměrné náhodné veličiny je korelační koeficient. Vzorec je tento:
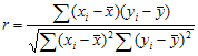
Pro odlišení od ostatních měr závislosti se někdy tento korelační koeficient nazývá Pearsonův.
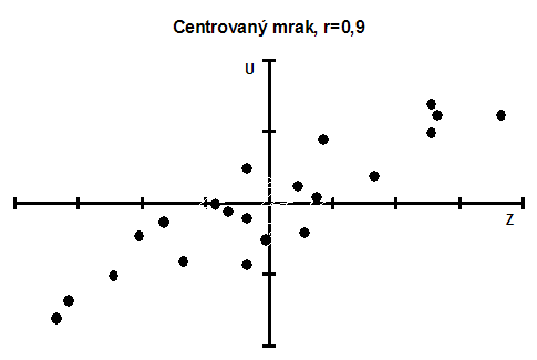
Pro objasnění toho, co tento vzorec znamená, si nejprve zdůvodníme, proč se v něm vyskytují průměry. Ty mají za úkol vycentrovat korelační mrak, to znamená posunout jej tak, aby počátek soustavy souřadnic byl umístěn uprostřed mraku. To je vidět na následujících dvou obrázcích.
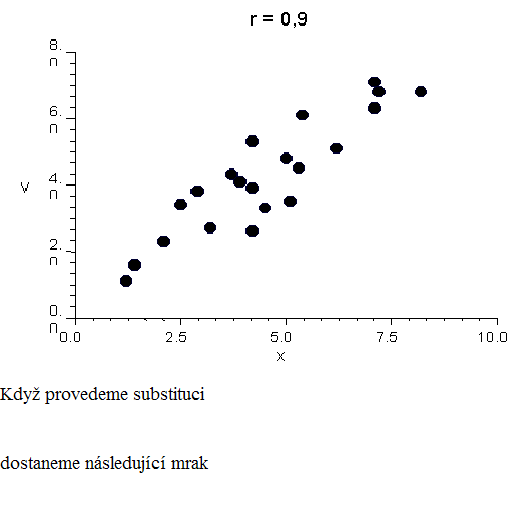
Vzorec má tvar
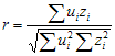
V čitateli je součet příspěvků jednotlivých bodů. Pokud jsou obě souřadnice kladné, je jejich součin kladný a jejich příspěvek je kladný. Když jsou obě souřadnice záporné, je jejich součin kladný a takový bod přispívá kladným příspěvkem. Když je jedna souřadnice kladná a ta druhá záporná, jejich součin je záporný a takový bod má záporný příspěvek. Velikost příspěvku jistě závisí na umístění vzhledem k počátku.
V našem příkladě převládají příspěvky kladné, tudíž korelační koeficient je kladný.
Korelační koeficient je bezrozměrný. Navíc při násobení veličiny kladnou konstantou se korelační koeficient nemění. Vynásobíme-li totiž veličinu u kladnou konstantou b, tuto konstantu můžeme vytknout jak v čitateli, tak ve jmenovateli, proto se vyruší a korelační koeficient se nemění.
Výraz ve jmenovateli zajistí, že korelační koeficient bude vždy v intervalu < -1; 1 >.
Z předcházejících úvah je vidět, že korelační koeficient blízký jedné dává vysokou závislost ve smyslu přímé úměrnosti, tedy čím větší je x, tím větší je také y. Korelační koeficient blízký -1 dává vysokou závislost opačnou, čím větší x, tím menší y.
Blok 0504 - Příklady - korelace
(Pro zobrazení odpovědi klikni na otázku.)
1) Pro korelační koeficient platí:A) je mírou síly lineární závislosti mezi dvěma proměnnými,
B) je vždy nezáporný,
C) nabývá hodnot od -1 do +1,
D) udává směrnici regresní přímky.
2) Rozhodněte, v kterém z následujících případů je vhodné použít korelační analýzu:
A) zkoumání vztahu mezi hladinou cukru a hladinou cholesterolu v krvi,
B) porovnání tepové frekvence před a po zátěži,
C) zjišťování závislosti mezi velikostí dávky anestetika a dobou jeho účinku,
D) porovnání velikosti červených krvinek dvou osob,
E) srovnání úspěšnosti dvou diagnostických metod,
F) porovnání průměrné doby hospitalizace ve dvou okresních nemocnicích.