Jednovýběrový t-test
Testy hypotézy o průměru (t-testy)
Jedním z nejdůležitějších přínosů do počtu pravděpodobnosti je práce Henry Gosseta, kterou publikoval pod jménem Student. Jestliže náhodné veličiny `x_1`, `x_2`, `…`, `x_n`, mají Gaussovo rozdělení s parametry `µ` a `σ` a jsou nezávislé, pak z nich utvořená náhodná veličina `t` má Studentovo rozdělení o `n−1` stupních volnosti.
Tato věta je velmi důležitá, protože umožňuje testování hypotéz o `µ` bez ohledu na to, jaký je parametr `σ`. Obvykle se spíš ptáme, jakou má rozdělení střední hodnotu a nezajímá nás tolik, jaká je jeho směrodatná odchylka. Právě tento parametr ve vzorci, kterým definujeme `T` (testové kritérium), není obsažen. Jedna realizace takové náhodné veličiny se uskuteční tak, že provedeme `n` nezávislých experimentů s Gaussovým rozdělením o stejných parametrech a vypočteme konkrétní hodnotu t podle uvedeného vzorce. Víme, že náhodná veličina `T` má Studentovo rozdělení o `n−1` stupních volnosti.
`t = \frac{\overline x - \mu _0 }{S/\sqrt n }`
Představme si, že známe µ0, `σ` znát nemusíme. Znalost Studentova rozdělení nám umožní testování nulové hypotézy `H_0`: `µ` = `µ_0`, kterou slovně vyjádříme tak, že rozdělení má střední hodnotu rovnu `µ_0`. Jestliže chceme testovat, musíme stanovit obor přijetí a obor zamítnutí. Obor přijetí je doplňkem oboru zamítnutí. Do oboru přijetí zahrneme ty hodnoty `t`, které se vyskytnou s větší pravděpodobností. Je vhodné si uvědomit několik věcí. Jednou z nich je to, že Studentovo rozdělení má zvonovitý tvar a že je jasné, kdy je hustota pravděpodobnosti v nějakém bodě větší než v jiném bodě. Pro libovolné stejně velké intervaly platí, že je-li hustota v prvním z intervalů vždy větší než v druhém intervalu, je pravděpodobnost padnutí náhodné veličiny do prvního intervalu větší než pravděpodobnost padnutí do druhého intervalu. Abychom to ještě lépe viděli, můžeme si číselnou osu rozdělit na libovolně malé ale stejně široké disjunktní intervaly a jim přiřadit pravděpodobnosti jako plochy pod křivkou hustoty.
Testujeme-li na hladině významnosti 5 %, musíme nalézt interval, do kterého padne náhodná veličina s pravděpodobností 0,95. Takový interval má zároveň obsahovat právě ty body, které mají větší hustotu než body mimo tento interval. Ze zvonovitosti a symetrie kolem nuly plyne, že to bude interval se středem v bodě nula. Plocha pod křivkou od nuly do pravého koncového bodu musí být rovna 0,95/2 = 0,475.
Totéž by platilo pro plochu pod křivkou od levého koncového bodu intervalu do nuly.
Ze symetrie víme (pomůže obrázek), že plocha pod křivkou od minus nekonečna do nuly je rovna 1/2. Rovněž plocha pod křivkou od nuly do nekonečna je 1/2. Hledáme-li pravý koncový bod intervalu, je to totéž jako hledat takový bod, pro který platí, že plocha pod křivkou od minus nekonečna do tohoto bodu je rovna 0,975=0,5+0,475. To je právě 97,5% kvantil Studentova rozdělení o `n-1` stupních volnosti a značí se `t_{n-1}`, 0,975.
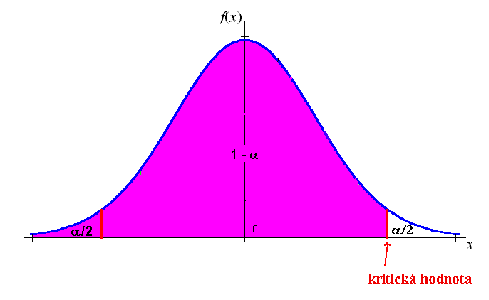
Díky symetrii hustoty je celý obor přijetí dán intervalem `(-t_{n-1},_{0,975}`; `t_n, _{0,975})` při 5% hladině významnosti, obor zamítnutí je dán sjednocením intervalů `(-∞ ; -t_{n-1}, _{0,975}) \cup ( t_{n-1}, _{0,975} ; ∞)`. Při 1% hladině významnosti je oborem přijetí interval `(-t_{n-1}, _{0,995}; t_{n-1}, _{0,995})` a oborem zamítnutí je interval `(- ∞; -t_{n-1},_{0,995}) \cup ( t_{n-1},_{0,995} ; ∞)`.
Kvantil Studentova rozdělení, který odděluje obor přijetí a zamítnutí se nazývá kritická hodnota. Kvantily Studentova rozdělení jsou tabelovány.
Některé tabulky uvádějí přímo hladinu významnosti v hlavičce, jiné uvádějí číslo `1-\alpha/2`, což je příslušný kvantil. Bývá v tom trochu nepořádek, proto je nutné si vždy zkontrolovat, o jakou tabulku se jedná. Pro `n > 30` Studentovo rozdělení již téměř splývá s rozdělením Gaussovým.
Jednovýběrový t-test
Chceme zjistit, zda střední hodnota zkoumané náhodné veličiny je rovna nám známé střední hodnotě `µ_0` a víme, že rozdělení zkoumané náhodné veličiny je normální. Statistický zápis je `H_0: µ = µ_0` . Zvolíme hladinu významnosti (obvykle 5%). Provedeme n nezávislých experimentů, jejichž výsledkem je n číselných hodnot. Vypočteme z nich výběrový aritmetický průměr a výběrovou směrodatnou odchylku a dosadíme je do vzorce
`t = \frac{\overline x - \mu _0 }{S/\sqrt n }`
Tím získáme hodnotu testového kritéria. Pomocí kvantilů Studentova rozdělení stanovíme obor přijetí a zjistíme, zda je testové kritérium v oboru přijetí či v oboru zamítnutí. Je-li testové kriterium v oboru přijetí, H0 nezamítneme, je-li v oboru zamítnutí, tak H0 zamítneme a přimeme alternativní hypotézu Ha `(H_a: µ≠ µ_0)`.
Postup je obdobný u všech testů: Stanovíme H0 (srovnávané charakteristiky jsou stejné, tj. jejich rozdíl se rovná nule), Ha a hladinu významnosti. Zvolíme testové kritérium, což je náhodná veličina. (Testové kriterium můžeme volit jen takové, u kterého je známo rozdělení. To je základní podmínkou pro to, abychom mohli určit obor přijetí.) Určíme obor přijetí a obor zamítnutí. Porovnáme testové kritérium s oborem přijetí a učiníme rozhodnutí o H0.
Příklad 1:
Ze vzorku krve jednoho pacienta byla změřena velikost 50 červených krvinek. Průměrná velikost u těchto 50 krvinek byla 7,13 mm a směrodatná odchylka 0,35 mm. Máme zjistit (na hladině významnosti 5 %), zda průměrná velikost červených krvinek tohoto pacienta odpovídá normě, tj. 7,2 mm.
Řešení příkladu 1:
Nejprve formulujeme H0: `µ = 7,2` [µm], Hą: `µ ≠ 7,2` [µm]. Hladina významnosti je 5 %. Nyní vypočteme testové kritérium: `t = |7,13 – 7,2|/(0,35/√50) = 1,41`.
Obor přijetí nulové hypotézy stanovíme buď pomocí tabulky kritických hodnot Studentova rozdělení nebo v Excelu tak, že funkcí TINV vypočítáme 97,5% kvantil Studentova rozdělení (zadáme pravděpodobnost = 0,05), pro počet stupňů volnosti 49. Hledaný kvantil je `t_{49}; _{0,975} = 2,01`. To znamená, že při platnosti nulové hypotézy je pravděpodobnost, že testové kriterium překročí číslo 2,01 rovna 0,025. Protože se jedná o rozdělení symetrické, víme že pravděpodobnost, že testové kriterium bude menší než –2,01 je také rovna 0,025. Jako obor přijetí vezmeme interval < –2,01; 2,01 >. Víme, že plocha pod křivkou je v oboru přijetí nulové hypotézy rovna 0,95. Obor zamítnutí je sjednocením dvou částí (–∞; 2,01) `\cup` (2,01; ∞). Známe též plochu pod křivkou vlevo od –2,01 a vpravo od 2,01. Dohromady je tato plocha 0,025 + 0,025 = 0,05, což je hladina významnosti.
Pro naše data je testové kriterium t rovno 1,41. Protože je v oboru přijetí, H0 na 5% hladině významnosti nezamítneme.
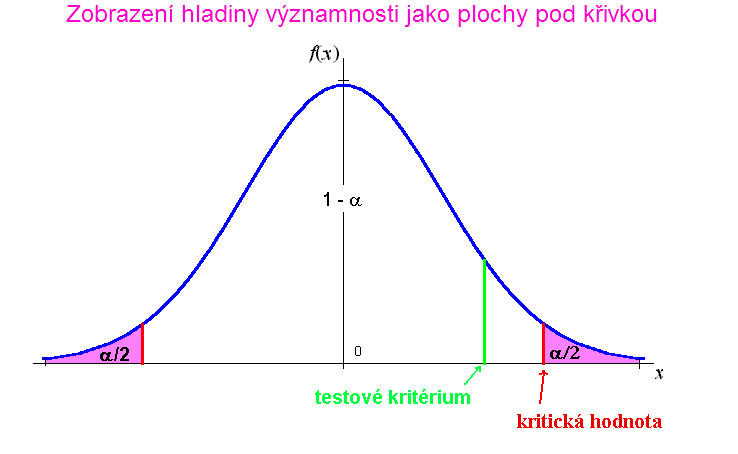
Můžeme na věc jít také jinak: Jaká je plocha pod křivkou od čísla 1,41 do nekonečna? Už víme, že je větší než 0,025, protože 1,41 je vlevo od 97,5-ti procentního kvantilu, ale představme si, že to nevíme a kvantil Studentova rozdělení neznáme. Označíme tuto plochu písmenem A. Vzhledem k tomu, že provádíme oboustranný test, musíme zahrnout také plochu od minus nekonečna do čísla -1,41. Ta bude stejná a jejich součtem dostaneme celkovou plochu 2A. Velikosti této plochy říkáme p-hodnota. Ručně je obtížné tuto plochu přesně vypočítat, ale na počítači (např. V Excelu pomocí funkce TDIST) to jde snadno. V našem případě je p-hodnota 0,16. Porovnáme ji s hladinou významnosti. Je-li p-hodnota menší než hladina významnosti, H0 zamítneme. Pokud tato podmínka není splněna, nemůžeme H0 na dané hladině významnosti zamítnout. V našem případě je 0,16 > 0,05, proto H0 na 5% hladině významnosti nezamítneme.
Pochopení souvislosti mezi p-hodnotou, testovým kritériem, hladinou významnosti a kritickou hodnotou usnadní následující obrázek.
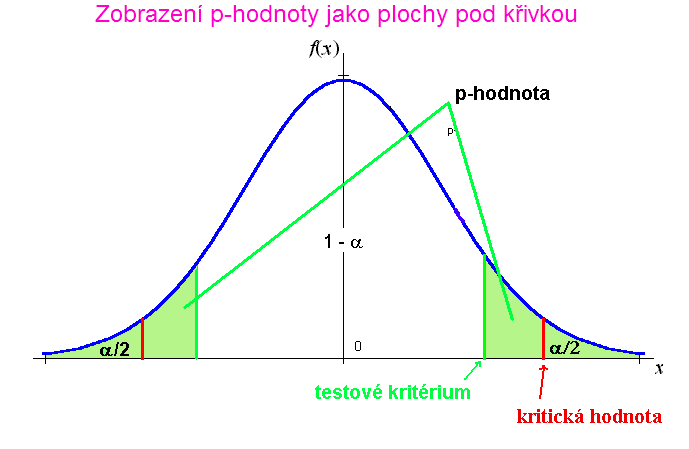
Statistické programy často uvádějí jako výsledek statistického testu p-hodnotu. Ta je definována jako nejmenší hladina významnosti, na které by se H0 dala zamítnout. Je tudíž jasné, že stačí jen znalost p-hodnoty a hladiny významnosti a můžeme provést rozhodnutí, aniž bychom znali testové kritérium a stanovovali obor přijetí a zamítnutí.
Připomeňme si znovu, že hladinu významnosti stanovujeme před testováním, neboť pravidla rozhodování mají být určena předem.
Příklad 2:
Průměrná hladina prothrombinu v normální populaci je 20,0 mg/100 mL plasmy. V souboru 30 pacientů, u nichž byl zjištěn nedostatek vitamínu K, byla průměrná hladina prothrombinu 18,3 mg/100 mL a směrodatná odchylka 3,8 mg/100 mL plasmy. Můžeme na základě těchto výsledků tvrdit, že průměrná hladina prothrombinu je u lidí s nedostatkem vitamínu K nižší než u normální populace? Rozhodnutí provedeme na 5% hladině významnosti.
Řešení příkladu 2:
Nejprve formulujeme H0 a Ha. Vzhledem k zadání problému bude alternativní hypotéza jednostranná. H0: µ = 20,0 [mg/100 mL], Ha: µ < 20,0 [mg/100 mL]. Hladina významnosti je 5 %. Nyní vypočteme testové kritérium: t = |18,3 – 20,0|/(3,8/√30) = 2,45.
Obor přijetí nulové hypotézy stanovíme buď pomocí tabulky kritických hodnot Studentova rozdělení nebo v Excelu tak, že funkcí TINV vypočítáme 95% kvantil Studentova rozdělení (zadáme pravděpodobnost = 0,1), pro počet stupňů volnosti 29. Hledáme kvantil 95%, protože tentokrát bude celý obor zamítnutí na jedné straně rozdělení hustoty. Hledaný kvantil je t29; 0,95 = 1,70. To znamená, že při platnosti nulové hypotézy je pravděpodobnost, že testové kriterium překročí číslo 1,70 rovna 0,05. Jako obor přijetí vezmeme interval <-∞; 1,70>. Plocha pod křivkou je v oboru přijetí nulové hypotézy rovna 0,95. Obor zamítnutí je (1,70; ∞). Plocha pod křivkou v oboru zamítnutí je 0,05, což je opět hladina významnosti.
Pro naše data je testové kriterium t rovno 2,45. Protože je v oboru zamítnutí, H0 na 5% hladině významnosti zamítneme.
Velikost p-hodnoty někdy svádí k chybným výrokům o tom, že střední hodnota je více či méně rovna nule a jim podobným. Důvod, proč jsou takové výroky nesmyslné, plyne z toho, že testujeme nulovou hypotézu, to jest zda platí nebo ne, čili výsledkem testování musí být rozhodnutí ve smyslu ano nebo ne. Není nic mezi. Říci, že něco je rovno nule více než něco jiného je nesmysl.

Párový test
Jako párový model označíme takový, při kterém jsou pozorování provedena ve dvojicích tak, že má smysl pozorované hodnoty v každém páru od sebe odečíst. Příkladem je provádění dvojic měření na stejných jedincích či předmětech za různých podmínek experimentu.
Typickým příkladem je měření nějaké veličiny před léčbou a po léčbě u stejných pacientů. Je možné hovořit o naměřené veličině před a po působení na tentýž subjekt a chceme zjistit, jaký má takové působení vliv.
Párování může vznikat také jinak. Uvedeme příklad příjmu manžela a manželky. Jestliže je zjišťujeme v jedné rodině, má smysl je porovnat a odečíst. Jedná se tedy o párový model.
Jiným příkladem může být porovnání opotřebení předního a zadního pláště jízdního kola, kde párování je zajištěno tím, že měření se provádí na pláštích na tomtéž kole. Vybíráme tedy dvojice plášťů najednou, nikoliv pláště předních kol zvlášť a pak pláště zadních kol u jiných jízdních kol.
Příklad:
U 10 osob měříme hladinu cholesterolu před léčbou a po léčbě.
Označme jako `x_i` měření před a `y_i` měření po léčbě. Dostáváme tak páry (`x_i`; `y_i`) měření pro `i = 1 , 2, …, N`. Takové páry tvoříme proto, abychom mohli definovat rozdíl `z_i = y_i - x_i`.
Dále už můžeme počítat jen s tímto rozdílem, protože `x_i` < `y_i` je totéž jako `z_i` > 0, také `x_i` > `y_i` je totéž jako `z_i` < 0 a nakonec `x_i` = `y_i` je totéž jako `z_i` = 0.
Podobně je možné zacházet s náhodnými veličinami `X_i` a `Y_i` , kde `i=1, 2, ... N`. Definujeme nové náhodné veličiny `Z_i = X_i - Y_i` a ptáme se, zda je `µ_Z` rovna nule. Experimenty navrhneme tak, že provádíme realizace dvojic náhodných veličin (`X_i` , `Y_i` ) a z nich dostaneme `Z_i = X_i - Y_i`.
Nulovou hypotézu o shodě středních hodnot můžeme zapsat jako:
H0: `µ_Z` = 0 nebo H0: `µ_X -µ_Y` = 0.
Vtip je v tom, že takovou H0 již umíme testovat pomocí jednovýběrového t-testu. V případě, že náhodné veličiny `Z_i` mají normální rozdělení s parametry `\mu =0` a nějaké `\sigma`, víme, že náhodná veličina
`\frac{\bar{Z}-\mu_Z}{S_z /\sqrt N}`
má Studentovo rozdělení o `N -1` stupních volnosti a umíme již stanovit obor přijetí a obor zamítnutí. Je to stejné jako u jednovýběrového t-testu, který v tomto případě použijeme k testování rozdílů.
Kdybychom měli k dispozici jen informaci o snížení nebo zvýšení hladiny cholesterolu, hovořili bychom o úspěchu nebo neúspěchu a mohli bychom použít tzv. znaménkový test (viz neparametrické testy), který je rovněž testem párovým. Pokud ale znaménkový test použijeme u spojité náhodné veličiny (jako v tomto případě), dojde ke ztrátě informací o velikosti snížení nebo zvýšení. Taková ztráta informace vede obvykle k tomu, že se sníží síla testu, což je nežádoucí.
Příklad:
U 20 osob zaznamenáváme krevní tlak v klidu a po zátěži. Pokud tlak krve skutečně měříme, ale zapisujeme pouze to, zda došlo ke zvýšení nebo snížení tlaku, můžeme k testování použít jen znaménkový test. Tím dojde ke ztrátě informace o velikosti změny tlaku. Bereme-li ale v úvahu naměřené hodnoty a použijeme párový t-test, ke ztrátě této informace nedochází a síla testu je větší.
Dvouvýběrový nepárový t-test a F-test
Nepárové testy
Nepárový čili dvouvýběrový model se realizuje tak, že se vybere `m` prvků z jedné populace a `n` prvků z druhé populace. Počty `m` a `n` nemusí být stejné. Podstatné je, že nemá smysl určovat rozdíl mezi prvky různých populací. To je to hlavní, čím se liší nepárový model od párového, i když je `m = n`.
Nepárovým t-testem testujeme shodu populačních aritmetických průměrů u dvou nezávislých skupin.
Postupy pro testování shody aritmetických průměrů jsou někdy komplikovanější. Při předpokladu normality obou rozdělení je dále nutné vědět, zda obě rozdělení mají stejné rozptyly. Pokud ano, použijeme jiný postup než když jsou rozptyly různé. Rozhodnutí o shodě rozptylů se provádí na základě testování hypotézy `σ_1^2 = σ_2^2` pomocí tzv. F-testu. Podle toho, jestli přijmeme či zamítneme tuto nulovou hypotézu, zvolíme vhodný test pro testování shody aritmetických průměrů, tj. hypotézy `µ_1 =µ_2`.
Výsledek testování hypotézy `σ_1^2 = σ_2^2` se tedy používá k tomu účelu, abychom správně rozhodli, zda k testování hypotézy `µ_1 =µ_2` použijeme nepárový t-test předpokládající shodné rozptyly obou rozdělení nebo nepárový t-test předpokládající rozptyly různé.
Bystrý student ví, že zamítnutí `σ_1^2 = σ_2^2` při platnosti `σ_1^2 = σ_2^2` na zadané hladině významnosti je chybou prvního druhu, přijetí `σ_1^2 = σ_2^2` při platnosti `σ_1^2<> σ_2^2` je chybou druhého druhu.
Odpověď na otázku, co se stane, když provedeme chybné rozhodnutí o rozptylech spočívá v tom, že oba postupy pro testování `µ_1 = µ_2` dávají numericky přibližně stejné výsledky, tudíž obvykle buď oba postupy tuto hypotézu zamítají nebo ji oba nezamítají. Jen když tyto dva postupy dávají odlišné rozhodnutí, uplatňuje se vliv toho, zda `σ_1^2 = σ_2^2` platí nebo ne.

ANOVA
Analýza rozptylu (angl. Analysis of Variance nebo ANOVA) je statistický test, který se používá k porovnání průměrů u několika (dvou nebo více) skupin dat. Přesněji řečeno: analýza rozptylu je prostředkem, který nám pomáhá zodpovědět otázku, zda se liší aritmetické průměry dvou nebo více populací. S pomocí analýzy rozptylu můžeme tedy například porovnat účinek několika léků na snížení hladiny cholesterolu nebo porodní hmotnost dětí matek kuřaček a nekuřaček. Jinými slovy: analýzou rozptylu můžeme například otestovat, zda snížení hladiny cholesterolu závisí na použitém léku nebo zda porodní hmotnost dětí závisí na tom, jestli je matka kuřačka. Jak je z uvedených příkladů patrné, naměřené hodnoty (hladiny cholesterolu, porodní hmotnosti) jsou realizacemi spojité náhodné veličiny, kdežto znak, který definuje porovnávané skupiny (podávaný lék, matka kuřačka/nekuřačka) je kategorický. Tomuto znaku, který určuje rozřazení do skupin, říkáme faktor. Je-li takový faktor jen jeden (jako v uvedených příkladech), mluvíme o jednofaktorové analýze rozptylu. Jestliže je faktorů více, hovoříme o vícefaktorové analýze rozptylu. Pokud například chceme ověřit, zda snížení hladiny cholesterolu závisí kromě na podaném léku také na pohlaví pacienta, musíme použít dvoufaktorovou analýzu rozptylu, neboť naměřené hodnoty cholesterolu rozřazujeme do skupin podle faktorů „lék“ a „pohlaví pacienta“.
Základní myšlenkou analýzy rozptylu je porovnání rozptylu uvnitř skupin jako míry pro variabilitu, která není ovlivněna faktorem, s rozptylem mezi skupinami, na němž by se vliv faktoru projevil.
V dalším se budeme věnovat jednofaktorové analýze rozptylu.
JEDNOFAKTOROVÁ ANALÝZA ROZPTYLU
Abychom mohli analýzu rozptylu s úspěchem použít, musí být splněny následující předpoklady:
- všechny porovnávané výběry (`i = 1,...,s`) pocházejí z populací s normálním rozdělením `N_i`( `µ_i` , `σ_i^2`)
- rozptyly všech těchto populací jsou shodné (tzv. homoskedasticita), tzn. `σ_1^2 = σ_2^2 = ...= σ_s^2`.
Postup testování:
- Jako u každého testu je nutné si nejprve stanovit NULOVOU a ALTERNATIVNÍ HYPOTÉZU a zvolit HLADINU VÝZNAMNOSTI. Jak vyplývá z předchozího, H0: `µ_1` = `µ_2` = ...= `µ_s` a Ha: alespoň dva aritmetické průměry `µ_i` jsou různé. Hladinu významnosti volíme nejčastěji 5%.
- Dále je třeba vybrat vhodné TESTOVÉ KRITÉRIUM a vypočítat jeho hodnotu.
Základní úvahy pro konstrukci testového kritéria
Při výpočtu testového kritéria vycházíme z porovnání variability uvnitř jednotlivých skupin a mezi skupinami. Jestliže je rozptyl mezi skupinami významně větší, než rozptyl uvnitř skupin, potom se jednotlivé skupiny od sebe (v průměru) významně liší a rozdělení do skupin podle daného faktoru má smysl.
Představme si situaci, kdy hodnoty měřeného znaku neovlivňuje nic jiného než jeden faktor, a to ten, podle něhož rozřazujeme měřená data do skupin. Potom by musely být všechny hodnoty v jedné skupině stejné. Tím pádem by rozdíly mohly být jen mezi skupinami, nikoliv uvnitř skupin samotných.
Rozptyl mezi skupinami, tj. ten, který se dá vysvětlit působením faktoru, nazýváme vysvětlený rozptyl.
V praxi se ale, díky individuálním rozdílům a chybám, liší i hodnoty v rámci jedné skupiny. Tyto interindividuální odlišnosti jsou zdrojem tzv. chybového rozptylu.
Testovým kritériem je poměr vysvětleného rozptylu a rozptylu chybového.
Výpočet hodnoty testového kritéria
- Výpočet rozptylu mezi skupinami, tj. vysvětleného rozptylu (angl. explained variance, treatment variance)
Jelikož máme k dispozici jenom výběry, můžeme provést pouze odhad vysvětleného rozptylu. Odhad provedeme tak, že všem naměřeným hodnotám v rámci jedné skupiny přiřadíme stejnou hodnotu, a to hodnotu rovnou výběrovému průměru v dané skupině. Tím „smažeme“ individuální rozdíly uvnitř jednotlivých skupin a získáme modelovou situaci, kdy jsou všechny hodnoty ve skupině stejné a rozdíly jsou pouze mezi skupinami. Z těchto „modelových“ dat vypočteme rozptyl tak, že vypočteme součet čtverců odchylek všech těchto „modelových“ hodnot od jejich průměru (tj. SCvysvetlený) a tento součet čtverců vydělíme počtem skupin sníženým o jedničku (tj. s-1), protože nám jde pouze o rozptyl mezi skupinami a ne mezi individuálními hodnotami. - Výpočet rozptylu uvnitř skupin, tj. chybového rozptylu (angl. error variance)
I tento rozptyl můžeme jenom odhadnout pomocí hodnot ve výběrech. Odhad provedeme následovně. Nejprve vypočteme výběrový rozptyl v každé skupině jako odhad variability uvnitř dané skupiny. Jedním z předpokladů analýzy rozptylu je, že (populační) chybový rozptyl je uvnitř všech skupin stejný. Jako odhad tohoto rozptylu tedy vezmeme průměr výběrových rozptylů všech skupin. - Mezi jednotlivými složkami rozptylu existuje vztah, který se dá nazvat aditivitou součtu čtverců. Součtem čtverců se rozumí čitatel vzorce pro výpočet rozptylu.
Platí:
SCcelkový = SCvysvetlený + SCchybový,
kde SCcelkový je čitatel celkového rozpylu skutečně naměřených dat a SCchybový je součet čtverců odchylek naměřených hodnot od jejich skupinového průměru pro všechny skupiny dohromady.
Jak bylo zmíněno výše, jako testové kritérium vezmeme podíl vysvětleného a chybového rozptylu:
`F = \frac{{\frac{{SC_{vysvetleny} }}{{s - 1}}}}{{\frac{{SC_{chybovy} }}{{n - s}}}}`
Tento podíl má F-rozdělení se stupni volnosti `\nu_{vysvětlené}` = `s – 1` a `\nu_{chybové}` = `n – s`, kde `n` je počet prvků ve všech výběrech dohromady.
- Vyhodnocení testu
Je-li hodnota testového kritéria menší nebo rovna kritické hodnotě (získáme ji z tabulek F-rozdělení nebo v excelu funkcí FINV), nulovou hypotézu o rovnosti všech průměrů nezamítneme (protože rozptyl mezi skupinami není statisticky významně větší než rozptyl uvnitř skupin).
Je-li hodnota poměru větší než kritická hodnota, nulovou hypotézu zamítneme a přijmeme hypotézu alternativní, která říká, že mezi skupinami jsou alespoň dvě, jejichž hodnoty se v průměru významně liší. Zda se ale od sebe liší jen dvě skupiny nebo jich je více a konkrétně které skupiny se liší od kterých, analýza rozptylu neříká. Je tedy jen prvním krokem, který má rozhodnout, je-li nutné další testování. V případě, ale opravdu jen v případě, že analýzou rozptylu zamítneme hypotézu o rovnosti průměrů všech skupin, použijeme další test, např. Tukeyův post-hoc test (je nad rámec této učebnice) , který dá odpověď na otázku, které skupiny se od sebe liší.
Poznámka:
Shodu dvou populačních průměrů můžeme testovat (a také obvykle testujeme) dvouvýběrovým t-testem. Dostaneme stejný výsledek jako při použití analýzy rozptylu. Porovnáváme-li ale průměry ve více než dvou skupinách, musíme použít analýzu rozptylu. (Kdybychom místo ANOVA použili pro každou dvojici skupin dvouvýběrový t-test, nevyhnuli bychom se kumulování pravděpodobnosti chyby a, tj. pravděpodobnosti, že v některém případě zamítneme pravdivou nulovou hypotézu.)
Pro ilustraci postupu při analýze rozptylu si uveďme příklad:
Porovnáváme (na 5% hladině významnosti) vliv tří různých léků na snížení systolického krevního tlaku (STK).
Pacienty jsme rozdělili do tří skupin podle toho, který z daných léků na snížení tlaku jim byl předepsán. Z každé skupiny jsme náhodně vybrali několik pacientů. Výsledky (snížení STK v mmHg po užití jedné denní dávky léku) uvádí následující tabulka.
Naměřené snížení STK (mmHg)
| skupina s1
užívající lék 1 |
skupina s2
užívající lék 2 |
skupina s3
užívající lék 3 |
| 20 | 40 | 30 |
| 20 | 40 | 30 |
| 30 | 50 | 40 |
| 30 | 50 | 40 |
| 40 | 60 | 50 |
| 30 | 50 | 50 |
| 30 | 50 | 40 |
| 40 | 60 | 20 |
| 10 | 30 | 70 |
| 50 | 70 | 30 |
Předpokládejme, že všechny tři zkoumané populace mají normální rozdělení. V praxi bychom tento předpoklad měli ověřit testem normality (např. d ’ Agostinovým testem).
Postup při analýze rozptylu:
1. Definujeme nulovou a alternativní hypotézu a hladinu významnosti:
H0: `µ_1` = `µ_2` = `µ_3` ,
Ha: alespoň dva populační aritmetické průměry jsou různé.
α = 0,05
2. Vypočteme hodnotu testového kritéria
`F = \frac{{\frac{{SC_{vysvetleny} }}{{s - 1}}}}{{\frac{{SC_{chybovy} }}{{n - s}}}}`
Průměrné snížení v jednotlivých výběrech je následující:
Postup výpočtu SCchybový:
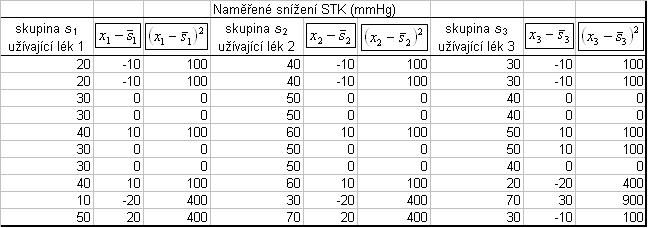
Součtem druhých mocnin všech rozdílů získáme SCchybový.
SCchybový = 4200.
Výpočet SCvysvetlený:
Jak už bylo zmíněno výše, průměrné snížení v jednotlivých výběrech je
Průměrné snížení ve všech výběrech dohromady je
Všem hodnotám v prvním výběru tedy přiřadíme hodnotu 30, všem hodnotám druhého výběru 50 a hodnotám třetího výběru 40 mmHg a vypočteme rozdíly těchto hodnot od celkového průměru a poté druhé mocniny těchto rozdílů.
Součtem druhých mocnin všech rozdílů získáme SCvysvetlený.
V našem příkladu má každý výběr 10 prvků. Můžeme tedy psát:
SCvysvetlený = 10(30 – 40)2 + 10(50 – 40)2 + 10(40 – 40)2 = 2000.
`F = \frac{{\frac{{2000}}{{3 - 1}}}}{{\frac{{4200}}{{30 - 3}}}}\dot = 6,4286`
V tabulkách (nebo pomocí funkce FINV v excelu) vyhledáme kritickou hodnotu F-rozdělení pro 2 a 27 stupňů volnosti. Fkritická = 3,3541.
Oborem přijetí je interval < 0; 3,3541 >. Hodnota testového kritéria 6,4286 je větší než kritická hodnota a spadá do oboru zamítnutí. Proto nulovou hypotézu na hladině významnosti 5% zamítneme a přijmeme hypotézu alternativní, která říká, že průměrné hodnoty se alespoň ve dvou skupinách liší.
Analýza rozptylu ukázala, že všechny tři léky nepůsobí na STK ve stejné míře. Neříká ale, zda se od sebe liší míra účinku u všech tří léků nebo jen u jedné konkrétní dvojice. K získání takovýchto informací bychom nyní museli použít ještě další test, tzv. post-hoc test. Post-hoc testů je celá řada (např. Bonferroniho test). Vycházejí často z porovnání každých dvou skupin dat pomocí t-testu, ale mají upravenou (zpřísněnou) hladinu významnosti podle počtu prováděných porovnání. Při provádění více statistických testů totiž roste pravděpodobnost, že někde vyjde statisticky významný výsledek pouze náhodou. Proto je žádoucí odpovídajícím způsobem hladinu významnosti korigovat.
UPRAVIT OTÁZKY
Blok 0503 - Příklady - parametrické testy
(Pro zobrazení odpovědi klikni na otázku.)
1) Jednovýběrový t-test lze použít?A) U ordinálních nebo kvantitativních dat.
B) Pouze u spojitých dat s normálním rozdělením.
C) K testování shody aritmetických průměrů zkoumané veličiny s předem známou hodnotou.
D) K testování shody populačního rozptylu s předem známou hodnotou.
2) Párový test se používá k testování:
A) se používá k testování shody aritmetických průměrů dvou nezávislých skupin pozorování.
B) se používá k testování nulovosti střední hodnoty rozdílů párových hodnot.
C) lze ho převést na jednovýběrový t-test.
3) Nepárový t-test se používá k testování:
A) shody populačních rozptylů u dvou nezávislých skupin pozorování.
B) shody výběrových rozptylů u dvou nezávislých skupin pozorování.
C) shody aritmetických průměrů u dvou nezávislých skupin.
D) shody aritmetických průměrů u párových pozorování.
4) Předpokládejme, že výška dospělých mužů v ČR má normální rozdělení s průměrnou hodnotou 177 cm. V souboru dvaceti náhodně vybraných profesionálních žokejů byla průměrná výška 167 cm a směrodatná odchylka 3,5 cm. Na 5% hladině významnosti ověřte předpoklad, že žokejové jsou v průměru menší než celonárodní průměr.
(Kritické hodnoty pro oboustranný test jsou:
pro 19 stupňů volnosti 2,093 ,
pro 20 stupňů volnosti 2,086,
pro 21 stupňů volnosti 2,080;
kritické hodnoty pro jednostranný test jsou:
pro 19 stupňů volnosti 1,729,
pro 20 stupňů volnosti 1,725,
pro 21 stupňů volnosti 1,721.)
5) F-test se používá k testování:
A) shody populačních rozptylů u dvou nezávislých skupin.
B) shody výběrových rozptylů u dvou nezávislých skupin.
C) shody populačních průměrů u dvou nezávislých skupin.
D) shody výběrových průměrů u dvou nezávislých skupin.
6) Při analýze rozptylu testujeme hypotézu o:
1. rovnosti výběrových průměrů u nezávislých výběrů
2. rovnosti výběrových průměrů u závislých výběrů.
3. rovnosti populačních průměrů.
4. rovnosti výběrových rozptylů.
5. rovnosti populačních rozptylů.
7) Alternativní hypotézou při ANOVA je tvrzení:
1. všechny porovnávané výběrové průměry se vzájemně liší.
2. všechny porovnávané populační průměry se vzájemně liší.
3. alespoň dva z porovnávaných populačních průměrů se liší.
4. alespoň dva z porovnávaných výběrových průměrů se liší.
5. všechny porovnávané rozptyly se liší.
6. alespoň dva z porovnávaných rozptylů se liší.
8) Testové kritérium v ANOVA je založené na vzájemném porovnání:
1. výběrových průměrů.
2. výběrových rozptylů.
3. variability mezi skupinami naměřených hodnot a uvnitř těchto skupin.
4. celkového průměru všech naměřených hodnot a průměrů uvnitř porovnávaných skupin.
9) Testování rovnosti průměrné tělesné výšky mužů a žen můžeme provádět:
1. párovým t-testem.
2. nepárovým t-testem.
3. analýzou rozptylu.
10) Který z následujících testů bychom měli použít pro srovnání působení čtyř různých hypnotik na míru prodloužení doby spánku?
1. Nepárový t-test.
2. Analýzu rozptylu.
3. F-test.