Když zahřejeme pevné těleso, tak se částice v látce, ze které je vyrobeno rozkmitají rychleji a zaberou více místa v objemu látky. Projeví se to změnou rozměrů tělesa. Změní-li se jeho délka a změnu ostatních rozměrů neuvažujeme, mluvíme o délkové teplotní roztažnosti. Setkáváme se s ní např. v létě, když vidíme, že jsou dráty elektrického vedení prověšeny, protože by v zimě popraskaly, kolejnice se na železnici připevňují k těžkým betonovým pražcům usazeným do štěrku, kovová potrubí musí mít pružná kolena, která umožňují vyrovnání teplotní roztažnosti. Dokonce i letadlo letící nadzvukovou rychlostí, kdy se jeho povrch třením o vzduch zahřívá na 100 °C, se za letu prodlouží téměř o půl metru.

Obr. 22: Kolejnice

Obr. 23: Most přes řeku
Označíme-li l0 délku tyče při teplotě 0 °C a její prodloužení při zahřátí o teplotu t jako Δl, pak můžeme prodloužení tělesa Δl vypočítat tak, že vynásobíme teplotní součinitel délkové roztažnosti α původní délkou l0 a teplotním rozdílem, o který se tyč zahřála.
prodloužení tyče = teplotní součinitel . původní délka . zvýšení teploty
`∆l = αl_0 ∆t ` [`\text [m]] `
Součinitel délkové teplotní roztažnosti těles α závisí na látce, z které je těleso vyrobeno. Udává nám, o jakou délku se prodlouží jeden metr určité látky při zahřátí o 1 °C.
hliník 24. 10-6 K-1 |
ocel 16,3. 10-6 K-1 |
Celou délku l, kterou má tyč zahřátá na teplotu t °C vypočítáme tak, že k původní délce l0 připočítáme prodloužení Δl
`l_t = l_0 + ∆l ` [`\text [m]] `
`l_t = l_0 + α l_0 * ∆t ` [`\text [m]] `
`l_t = l_0 * ( 1 + α ∆t) ` [`\text [m]] `
Jestliže se teplota tyče zmenšuje, zkrátí se její délka podle vzorce:
`l_t = l_0 (1 - α ∆t) ` [`\text [m]] `
Využití teplotní délkové roztažnosti: požární hlásiče, termostaty v elektrických topidlech, vařičích a žehličkách, bimetalové teploměry.

Obr. 24: Regulace teploty v žehličce
Řešené úlohy
Úloha č. 1 
OBJEMOVÁ TEPLOTNÍ ROZTAŽNOST PEVNÝCH LÁTEK
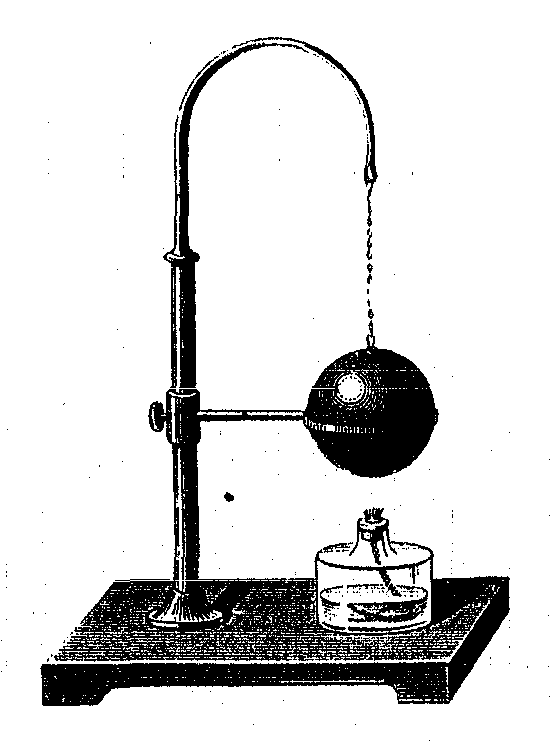
Obr. 25: Zahřátá ocelová kulička nepropadne prstencem
Zahřejeme-li silnou kovovou tyč, zjistíme, že se roztáhne nejen do délky, ale že se zvětší také její šířka a výška. Podobně se chová i většina pevných látek, při zahřívání mění svoje rozměry všemi směry stejně. Při zahřívání se zvětšuje jejich objem, při ochlazování se jejich objem zmenší.
Všechny pevné látky ale svůj objem nemění stejně. Látky, které se roztahují všemi směry stejně, nazýváme teplotně izotropní. Jiné látky se roztahují v různých směrech různě, takové látky nazýváme teplotně anizotropní. Přesným měřením a opakovanými výpočty bylo zjištěno, že součinitel teplotní objemové roztažnosti β je u izotropních i anizotropních látek roven přibližně trojnásobku středního součinitele teplotní délkové roztažnosti α.
pro pevné látky β≅3α
Jestliže ohřejeme pevné těleso z teploty t1 na teplotu t2 o teplotní rozdíl Δt, zvětší se objem tělesa podle vzorce
`V_t = V_0 *( 1+ beta∆t)`
Zvláštností teplotní objemové roztažnosti pevných látek je chování některých krystalů při změně jejich teploty. Tyto krystaly totiž mění svoji délku jinak než šířku a výšku. Mají tedy jen dva různé směry roztažnosti. A jiné krystaly dokonce při zahřívání jeden rozměr zkracují a svůj objem zmenší (jodid stříbrný). J. P. Joule jako první změřil, že se např. kaučuková hadice zkrátí, když jí prochází proud horké páry, ale její průřez se zvětší.
Teplotní objemová roztažnost pevných látek v praxi:
- Když se v automobilovém motoru příliš zahřeje píst, roztáhne se a uvázne ve válci.
- Dráty elektrického vedení jsou v létě víc prověšené, v zimě naopak natažené.
- Kolejnice i ocelové konstrukce mostů se s rostoucí teplotou prodlouží.
K teplotní objemové roztažnosti ale dochází i u kapalin a plynů:
- Zamrzne-li voda v trhlině skály, roztrhne led svým roztahováním skálu.
- Když se zvýší teplota tak rtuť v teploměru zvětší svůj objem a stoupá skleněnou trubičkou nahoru.
- Kdyby v zimě zmrzla čistá voda v chladičích aut, roztrhla by chladič.
Jestliže se zahříváním tělesa mění jeho objem, částice látky mění svoji vzájemnou vzdálenost a mění se i hustota látky. Hmotnost látky se však zachovává.
Zahříváním těles se hustota látek zmenšuje, ochlazováním zvětšuje.
`rho_t = rho_0 *( 1- beta∆t)`
Řešené úlohy
Úloha č. 1 
Úloha č. 2 
 Teplotní délková a objemová roztažnost
Teplotní délková a objemová roztažnost