Předmluva
Teoretické odborné předměty
Od 1. září školního roku 2009/2010 zavádíme na naší Střední škole polytechnické, Brno, Jílová 36g, nové školní vzdělávací programy, jeden z nich pro tříletý učební obor 26-51-H/02 ELEKTRIKÁŘ – SILNOPROUD. Cílem jejich zavádění je, aby absolvent, jako středoškolsky vzdělaný odborník se vzděláním všeobecným i odborným, po úspěšném vykonání závěrečné zkoušky a po příslušné praxi byl připraven instalovat, opravovat, udržovat a kontrolovat elektrické spotřebiče, rozvody elektrické energie a další zařízení, která využívají ke své činnosti elektrickou energii. Absolvováním tohoto oboru získává žák odbornou způsobilost v elektrotechnice – stává se osobou znalou. Pro samostatnou činnost v oblasti rozvodu elektrické energie, montáže, údržby a oprav elektrických zařízení je po získání praxe možno následně úspěšně vykonat zkoušky dle právních předpisů pro získání příslušné odborné způsobilosti v elektrotechnice, a stát se osobou znalou s vyšší kvalifikací. Náplní tohoto učebního textu pro první ročník je přehled učiva základů elektrotechniky a dále norem často využívaných v elektrotechnické praxi.
PaedDr. Petr Duchek
Základní veličiny a jednotky, jejich převody
- Vyjmenujte sedm základních veličin a jednotek soustavy SI
| délka | metr | m |
| hmotnost | kilogram | kg |
| čas | sekunda | s |
| elektrický proud | ampér | A |
| teplota | kelvin | K |
| látkové množství | mol | mol |
| svítivost | kandela | cd |
- Vyjmenujte násobky a díly jednotek podle předpon:
T |
tera |
1012 |
G |
giga |
109 |
M |
mega |
106 |
k |
kilo |
103 |
m |
mili |
10-3 |
µ |
mikro |
10-6 |
n |
nano |
10-9 |
p |
piko |
10-12 |
- Praktický příklad převodů jednotek – převeďte 10 kiloampérů na ampéry a miliampéry:
10 kA = 10 000 A = 10 000 000 mA
- Praktický příklad převodů jednotek – převeďte 155 megavoltů na volty a kilovolty:
155 MV = 155 000 000 V = 155 000 kV
- Praktický příklad převodů jednotek – převeďte 63 mikroampérů na ampéry a miliampéry:
63 µA = 0, 000 063 A = 0,063 mA
- Praktický příklad převodů jednotek – převeďte 22 kiloohmů na ohmy a megaohmy:
22 kΩ = 22 000 Ω = 0,022 MΩ
- Praktický příklad převodů jednotek – převeďte 0,022 ampérů na miliampéry a mikroampéry:
0,022 A = 22 mA = 22 000 µA
- Praktický příklad převodů jednotek – převeďte 2·105 wattů na watty pomocí nul a na kilowatty:
2 `*` 105 W = 200 000 W = 200kW
- Praktický příklad převodů jednotek – převeďte 500 megaohmů na ohmy pomocí nul a pomocí mocniny deseti:
500 MΩ = 500 000 000 Ω = 5`*`108Ω
Vodiče, polovodiče, nevodiče
- Vysvětlete pojem elektronová teorie:
Látky jsou složeny z molekul a molekuly z atomů – atom má jádro obsahující kladné protony a neutrální neutrony a obal složený ze záporných elektronů, tyto elektrony vytvářejí kolem jádra takzvané slupky, neboli sféry. U některých látek, např. kovů, je v poslední sféře malý počet elektronů a ty jsou velmi slabě vázány k jádru atomu – mohou být vnějšími elektrickými silami snadno uvolněny a stávají volnými – v pevných vodičích umožňují vznik elektrického proudu.
- Jak rozdělujeme látky podle elektrické vodivosti:
Dělíme je na vodiče – obsahují větší množství volných nositelů elektrických nábojů, dále na nevodiče neboli izolanty – obsahují nepatrné množství volných nositelů elektrických nábojů a dále na polovodiče – vedou elektrický proud jen za určitých podmínek.
- Čím je vytvářen elektrický proud v pevných vodičích:
Elektrický proud je zde tvořen uspořádaným tokem volných elektronů.
- Jaké vlastnosti má elektrovodná měď:
Má červenohnědou barvu, bod tavení 1083 °C, měrnou hmotnost 8960 kg/m3, měrný elektrický odpor 0,0178 Ωmm2/m, používá se na výrobu elektrických vodičů.
- Jaké vlastnosti má elektrovodný hliník:
Má stříbřitě lesklou barvu, bod tavení 659 °C, měrnou hmotnost 2700 kg/m3, měrný elektrický odpor 0,0285 Ωmm2/m, používá se na výrobu elektrických vodičů.
Stejnosměrný proud
- Z čeho se skládá jednoduchý elektrický obvod:
Elektrický obvod se skládá z napájecího elektrického zdroje, propojovacích elektrických vodičů a elektrického spotřebiče.
- Nakreslete schéma jednoduchého elektrického obvodu:
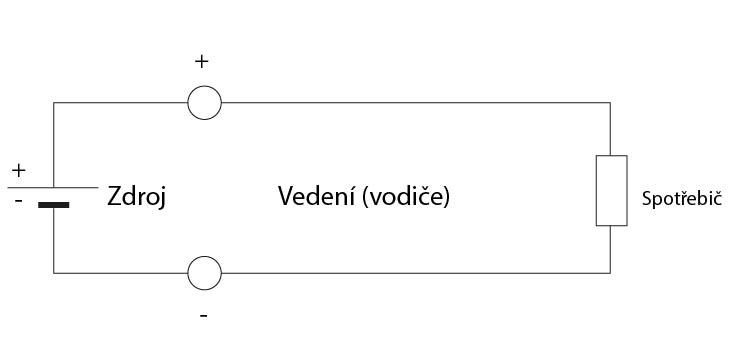
- Vysvětlete pojem elektrický odpor:
Různé materiály, kterými teče elektrický proud, kladou tomuto procházejícímu elektrickému proudu (např. v pevných vodičích pohybu elektronů) různé překážky, tedy kladou průchodu elektrického proudu určitý elektrický odpor.
- Vysvětlete pojem měrný elektrický odpor, neboli rezistivita:
V technické praxi je to odpor vodiče dlouhého jeden metr, o průřezu jeden milimetr čtvereční, při teplotě 20 °C.
- Jakou jednotku má měrný elektrický odpor neboli rezistivita:
V technické praxi je to jeden Ω mm2/m, čteme ohm milimetr čtvereční na metr.
- Vysvětlete, kdy má vodič odpor jednoho ohmu:
Vodič má elektrický odpor jednoho ohmu, jestliže jím při napětí jednoho voltu prochází proud jeden ampér.
- Vysvětlete pojem zdroj elektrického napětí:
Elektrický zdroj je zařízení, které má za úkol mezi dvěma místy (např. svorkami zdroje) vytvářet a trvale udržovat elektrické napětí vlivem vnějších neelektrických sil.
- Vysvětlete pojem elektrické napětí:
Elektrické napětí je definováno prací, potřebnou k přemístění elektrického náboje.
- Vysvětlete, jak je definováno napětí jednoho voltu:
Jeden volt je definován prací jednoho joulu, která je potřebná k přemístění náboje jednoho coulombu.
- Vysvětlete pojem elektrická vodivost:
Elektrická vodivost je rovna převrácené hodnotě elektrického odporu, je to tedy opačná vlastnost než elektrický odpor.
- Vysvětlete pojem závislost na teplotě:
Měřením elektrického odporu různých elektrických vodičů při různých teplotách je možno zjistit, že u některých z nich elektrický odpor se stoupající teplotou narůstá, u jiných naopak jejich elektrický odpor se stoupající teplotou klesá. Vysvětlujeme si to tak, že s nárůstem teploty se více rozkmitají částice hmoty (atomy i molekuly) a např. u některých pevných vodičů naroste počet srážek volných elektronů a jejich elektrický odpor se zvětší, u jiných pevných vodičů se naopak uvolní další elektrony z vnějších slupek atomů a jejich elektrický odpor se zmenší.
- Vysvětlete pojem kladný teplotní součinitel odporu:
U některých látek s narůstající teplotou jejich elektrický odpor roste, o těchto látkách říkáme, že mají kladný teplotní součinitel odporu.
- Vysvětlete pojem záporný teplotní součinitel odporu:
U některých látek s narůstající teplotou jejich elektrický odpor klesá, o těchto látkách říkáme, že mají záporný teplotní součinitel odporu.
- Vysvětlete pojem Ohmův zákon a nakreslete k němu schéma:
Je to základní zákon elektrotechniky, vyjadřuje skutečnost, že elektrický proud I v elektrickém obvodu je přímo úměrný elektrickému napětí U, grafem této úměry je přímka procházející počátkem souřadnicového systému a znázorňuje veličinu zvanou elektrický odpor R.
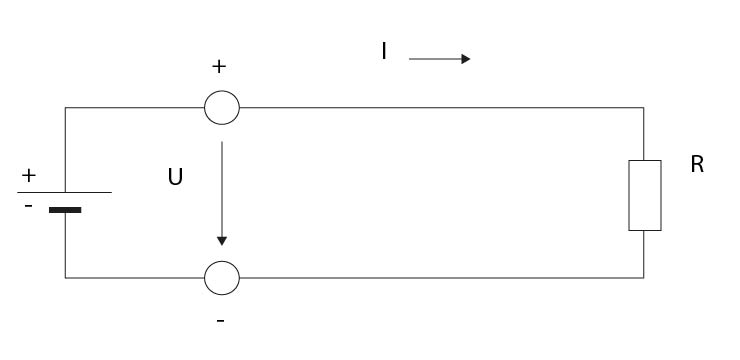
- Kdo byl Georg Simon Ohm:
Německý fyzik Georg Simon Ohm se narodil 16. března 1787 v rodině zámečnického mistra v Erlangenu v Německu (nedaleko Norimberku). Brzy mu zemřela matka. Jeho otec se o něj příkladně staral a dokonce se učil matematiku a fyziku, aby synovi pomohl při studiích. Georg Simon Ohm začal v roce 1805 studovat matematiku, fyziku a filozofii na univerzitě v Erlangenu. Kvůli nedostatku peněz studia po roce přerušil a začal ve Švýcarsku učit matematiku. V roce 1811 se Ohm na univerzitu vrátil a v roce 1813 studia ukončil. Ve svém životě trpěl Ohm nedostatkem finančních prostředků – jak při studiích, tak i při své činnosti jako středoškolského profesora. Podmínky pro vědeckou práci neměl ideální.
Od roku 1817 působil Ohm na gymnáziu v Kolíně nad Rýnem. Zde učinil Ohm své největší objevy. Škola byla na tehdejší dobu poměrně dobře vybavená. Ohm se zaměřil na oblast fyziky, byl ovlivněn objevem magnetických účinků elektrického proudu. V roce 1826 zveřejnil Ohm své poznatky v časopise Journal für Chemie und Physik. Ohm zůstal mnoho let nepochopen a kritizován. Jednou z překážek byla také neexistence absolutní soustavy elektrických veličin.
V letech 1833–1849 působil Ohm jako profesor fyziky na polytechnice v Norimberku, kde byl od roku 1839 rektorem. Prvního významného ocenění se mu dostalo až v roce 1841 – (Ohm) obdržel vyznamenání od Londýnské Královské společnosti – Copleyovu medaili. V roce 1842 byl Georg Simon Ohm zvolen za člena Královské společnosti.
V roce 1849 byl Ohm povolán na mnichovskou univerzitu a tím se mu splnilo jeho velké přání. Georg Simon Ohm zde působil nejprve jako mimořádný profesor a od roku 1852 jako profesor řádný.
Georg Simon Ohm zemřel 7. července 1854 v Mnichově ve věku 67 let.
- Vyjádřete výpočet proudu z Ohmova zákona:
`\text {I} = \text {U}/ \text {R}` ( A; V, Ω)
I...elektrický proud
U...elektrické napětí
R...elektrický odpor
- Vyjádřete výpočet napětí z Ohmova zákona:
`\text {U} = \text {R} * \text {I}` ( V; Ω, A)
U...elektrické napětí
R...elektrický odpor
I...elektrický proud
- Vyjádřete výpočet odporu z Ohmova zákona:
`\text {R} = \text {U}/ \text {I}` ( Ω; V, A)
R...elektrický odpor
U...elektrické napětí
I...elektrický proud
- Jak se značí elektrická vodivost a jakou má jednotku:
Elektrická vodivost se značí G, její jednotkou je 1 S (siemens).
- Vyjádřete matematicky vztah mezi elektrickou vodivostí a elektrickým odporem:
`\text {G} = \text {1}/ \text {R}` ( S; –, Ω)
G...elektrická vodivost
R...elektrický odpor
- Vyjádřete matematicky vztah mezi elektrickým odporem a elektrickou vodivostí:
`\text {R} = \text {1}/ \text {G}` ( Ω; –, S)
R...elektrický odpor
G...elektrická vodivost
- Výpočet odporu vodiče z jeho rozměrů a materiálu:
`\text {R} = ρ * \text {l}/ \text {S}` (Ω; Ωmm2 / m, m, mm2)
R...odpor vodiče
ρ...měrný elektrický odpor vodiče, pro měď má hodnotu 0,0178 Ωmm2/m, pro hliník má hodnotu 0,0285 Ωmm2/m
l...délka vodiče
S...průřez vodiče
- Výpočet odporu vodiče v závislosti na jeho teplotě:
`\text {R}_2 = \text {R}_1 * [\text {1} + \text {α} * ( \text {ϑ}_2 - \text {ϑ}_1)] ` (Ω; Ω, –, 1/ °C , °C, °C )
R2...odpor vodiče při teplotě v2
R1...odpor vodiče při teplotě 20 °C
α...teplotní součinitel odporu, pro běžné vodiče bývá 0,004 1/ °C
ϑ2...teplota vodiče jiná než 20 °C
ϑ1...teplota vodiče 20 °C
- Vysvětlete pojem řazení odporů do série:
Toto zapojení se provede tak, že konec prvního odporu se spojí se začátkem druhého odporu.
- Jak se jinak řekne řazení odporů do série:
Tomuto zapojení se také říká zapojení odporů za sebou.
- Nakreslete schéma řazení odporů do série:
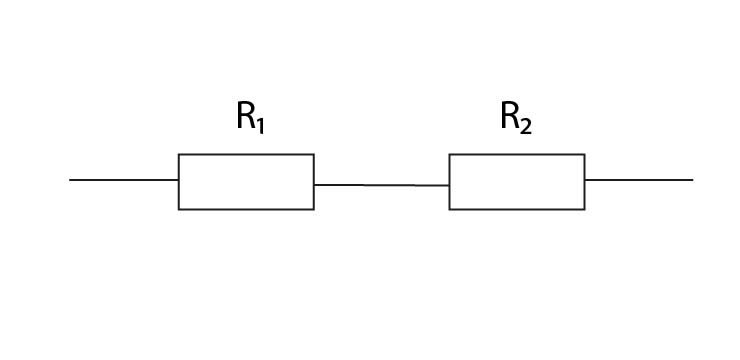
- Výpočet výsledného odporu dvou odporů zapojených do série:
R= R1 + R2 ( Ω; Ω, Ω)
- Vysvětlete pojem řazení odporů paralelně:
Toto zapojení se provede tak, že začátek prvního odporu se spojí se začátkem druhého odporu a konec prvního odporu se spojí s koncem druhého odporu.
- Nakreslete schéma řazení odporů paralelně:
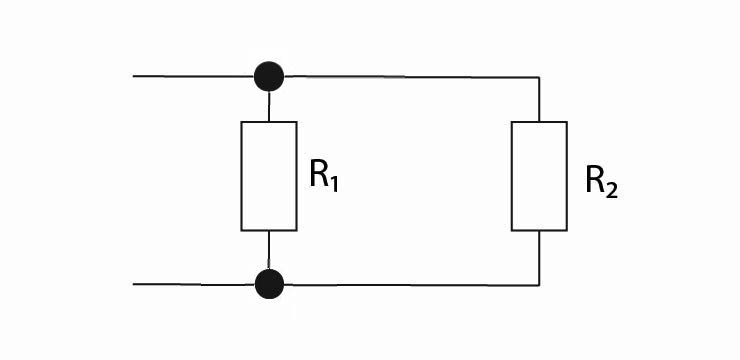
- Výpočet výsledného odporu dvou odporů zapojených paralelně:
`\text {R} = {\text {R}_1 * \text {R}_2} / {(\text {R}_1 + \text {R}_2)}` ( Ω; Ω, Ω, Ω, Ω)
R...výsledný odpor
R1...odpor prvního rezistoru
R2...odpor druhého rezistoru
- Jak se jinak řekne řazení odporů paralelně:
Tomuto zapojení se také říká zapojení odporů vedle sebe.
- Vysvětlete pojem Kirchhoffův zákon o proudu:
Důležitým pojmem je zde tzv. uzel, tedy místo vodivě spojující příslušné vodiče do jednoho bodu. Součet všech proudů do uzlu vstupujících se rovná součtu všech proudů z uzlu vystupujících.
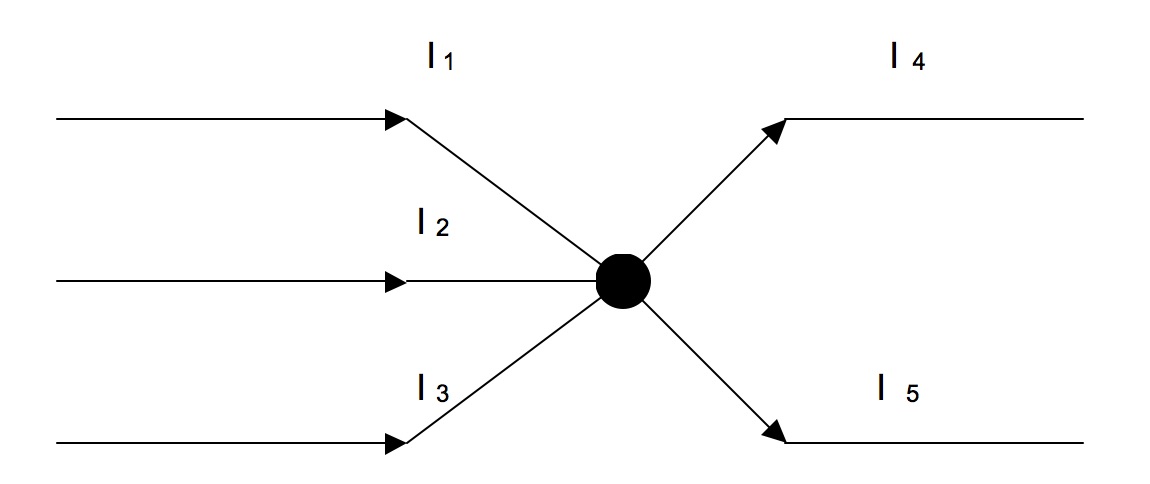
- Napište rovnici a jednotky Kirchhoffova zákona o proudu dle výše uvedeného schéma:
I1 + I2 + I3 = I4 + I5 (A, A, A; A, A)
I1...proud první větve
I2...proud druhé větve
I3...proud třetí větve
I4...proud čtvrté větve
I5...proud páté větve
- Vysvětlete pojem Kirchhoffův zákon o napětí:
Součet všech napětí na sériově zapojených zdrojích v uzavřeném obvodu se rovná součtu všech napětí na sériově zapojených spotřebičích k těmto zdrojům.
- Kdo byl Gustav Robert Kirchhoff:
Gustav Robert Kirchhoff se narodil 12. března 1824 v Königsbergu (Prusko, nyní Kaliningrad v Rusku). Jeho profesorem byl K. F. Gauss.
Od roku 1854 byl Kirchhoff profesorem fyziky na univerzitě v Heidelbegu.
Kromě elektrických jevů se zbýval i dalšími oblastmi fyziky a v roce 1859 dokázal zákon o vztahu mezi emisí a absorbcí světla. Spolu s Bunsenem rozvinuli metodu spektrální analýzy.
Touto metodou je možné určit složení hvězd. V letech 1860–61 pomocí spektrální analýzy objevili dva nové chemické prvky (cesium a rubidium).
Kirchhoff dále definoval pojem černého tělesa a ukázal principiální význam úlohy určit jeho spektrum. Při studiu tepelného záření Kirchhoff zjistil, že v každé dutině obklopené stejně teplými tělesy vznikne univerzální záření (záření černého tělesa) závislé jen na teplotě stěn, ne však na jejich druhu, a že na toto dutinové záření lze vztáhnout intenzitu vyzařování jakéhokoliv tělesa, jsou-li známy jeho absorpce a index lomu.
Roku 1874 vydává Kirchhoff Přednášky o mechanice, roku 1875 se stal členem Královské společnosti.
Zemřel 17. října 1887 v Berlíně.
- Nakreslete schéma pro Kirchhoffův zákon o napětí:
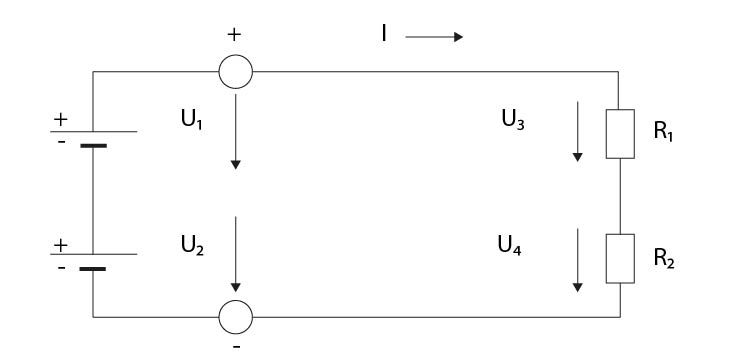
- Napište rovnici a jednotky Kirchhoffova zákona o napětí dle výše uvedeného schéma:
U1 + U2= U3 + U4 (V, V; V, V)
U1...napětí jednoho zdroje
U2...napětí druhého zdroje
U3...napětí jednoho rezistoru
U4...napětí druhého rezistoru
- Vysvětlete pojem elektrický výkon:
Elektrický výkon daného spotřebiče je závislý na velikosti k němu připojeného elektrického napětí a na velikosti jím protékajícího elektrického proudu.
- Jak se značí elektrický výkon a jakou má jednotku:
Elektrický výkon se značí P a jeho jednotkou je 1 W (watt).
- Jak se vypočítá elektrický výkon:
P= U `*` I (W; V, A)
P...elektrický výkon
U...elektrické napětí
I...elektrický proud
- Vysvětlete pojem elektrická účinnost elektrického zařízení:
Elektrická účinnost je dána podílem dodaného elektrického výkonu, kterému říkáme příkon, a užitečného výkonu na výstupu daného elektrického zařízení.
- Jak se značí účinnost elektrického zařízení a jakou má jednotku:
Elektrická účinnost se značí η (čteme éta) a nemá žádnou jednotku.
- Jak je důležitá účinnost elektrického zařízení:
Účinnost elektrických zařízení má vliv na hospodárnost a je-li vysoká, umožňuje menší čerpání energetických surovin, a tak přispívá k ochraně životního prostředí.
- Jak se vypočítá účinnost elektrického zařízení:
`\text {η} = \text {P}_2/ \text {P}_1` ( - ; W, W )
η...účinnost
P2...užitečný výkon na výstupu daného elektrického zařízení
P1...příkon
- Jak se vypočítá účinnost elektrického zařízení v procentech:
`\text {η} = \text {P}_2/ \text {P}_1 * 100` ( %; W, -, W )
η...účinnost
P2...užitečný výkon na výstupu daného elektrického zařízení
P1...příkon
- Vysvětlete pojem elektrická práce elektrického zařízení:
Elektrická práce daného spotřebiče je závislá na velikosti k němu připojeného elektrického napětí a na velikosti jím protékajícího elektrického proudu po určitou dobu.
- Jak se značí elektrická práce a jakou má jednotku:
Elektrická práce se značí A a její jednotkou je 1 J (joule).
- Jak se vypočítá eletrická práce:
A= U `*` I `*` t (J; V, A, s)
A...elektrická práce
U...elektrické napětí
I...elektrický proud
t...čas
- Jak se vypočítá elektrická práce pomocí elektrického výkonu:
A= P `*` t (J; W, s)
A...elektrická práce
P...elektrický výkon
t...čas
- Vysvětlete pojem elektrické teplo:
Toto teplo vzniká ve vodiči průchodem elektrického proudu, kdy elektrony v pevných vodičích předávají část své energie ostatním částicím hmoty v těchto vodičích. Tomuto teplu říkáme Lenz-Jouleovo teplo.
- Jak se značí elektrické teplo a jakou má jednotku:
Elektrické teplo se značí Q a jeho jednoutkou je 1 J (joule).
- Jak zní Lenz-Jouleův zákon:
Teplo, které vzniká ve vodiči průchodem elektrického proudu, je přímo úměrné součinu elektrického napětí, elektrického proudu a času.
- Jak se vypočítá elektrické teplo:
Q= U `*` I `*` t (J; V, A, s)
Q...elektrické teplo
U...elektrické napětí
I...elektrický proud
t...čas
- Jak se vypočítá elektrické teplo pomocí elektrického výkonu:
Q= P `*` t (J; W, s)
Q...elektrické teplo
P...elektrický výkon
t...čas
- Vysvětlete pojem elektrická energie:
Práce, kterou vykoná elektrický proud ve vodiči, je rovna spotřebované elektrické energii.
- Jak se značí elektrická energie a jakou má jednotku:
Elektrická energie se značí W a její jednotkou je 1 J (joule).
- Jak se vypočítá elektrická energie:
W= U `*` I `*` t (J; V, A, s)
W...elektrická energie
U...elektrické napětí
I...elektrický proud
t...čas
- Jak se vypočítá elektrická energie pomocí elektrického výkonu:
W= P `*` t (J; W, s)
W..elektrická energie
P...elektrický výkon
t...čas
- Jakou jinou jednotku může mít elektrická energie:
Z výše uvedeného vzorce vyplývá, že jednotak jeden joule je rovna jednotece jedna wattsekunda:
1J = 1Ws
Tato jednotka wattsekunda je pro technickou praxi příliš malá, proto se užívá jednotka jedna watthodina:
1Wh = 3600 Ws
Ještě větší jednotkou je kilowatthodina, případně megawatthodina:
1kWh = 1000 Wh = 3600000 Ws
1MWh = 1000 kWh = 3600000000 Ws
- Vysvětlete pojem řazení zdrojů:
Někdy nám nestačí elektrické napětí či elektrický proud jednoho napájecího elektrického zdroje, a proto připojujeme k danému elektrickému obvodu i několik napájecích zdrojů, které můžeme vzájemně spojovat různým způsobem.
- Vysvětlete pojem řazení zdrojů do série:
Tomuto zapojení se také říká zapojení za sebou a provede se tak, že jeden pól prvního zdroje se spojí s opačným pólem druhého zdroje.
- Nakreslete schéma řazení zdrojů do série:
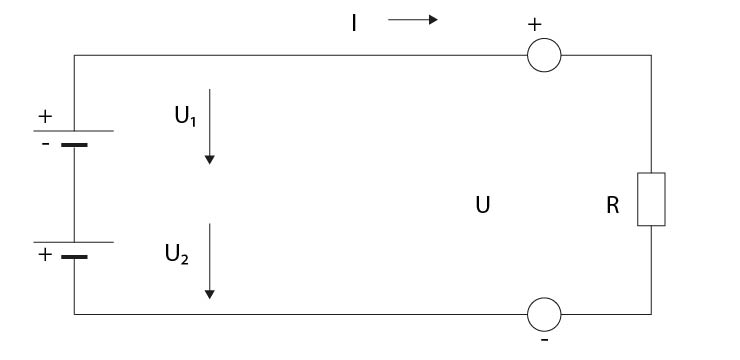
- Jaký proud teče obvodem při řazení zdrojů do série:
Obvodem teče pouze jeden proud I, který protéká stejný jak každým z obou zdrojů, tak také spotřebičem R.
- Jaké napětí je na výstupních svorkách obvodu při řazení zdrojů do série:
Napětí na výstupních svorkách se rovná součtu napětí všech seriově řazených zdrojů.
- Výpočet výsledného napětí dvou zdrojů zapojených do série:
U= U1 + U2 (V; V, V)
U1...napětí prvního zdroje
U2...napětí druhého zdroje
- Vysvětlete pojem řazení zdrojů paralelně:
Tomuto zapojení se také říká zapojení zdrojů vedle sebe a provede se tak, že jeden pól prvního zdroje se spojí se stejným pólem druhého zdroje.
- Nakreslete schéma řazení zdrojů paralelně:
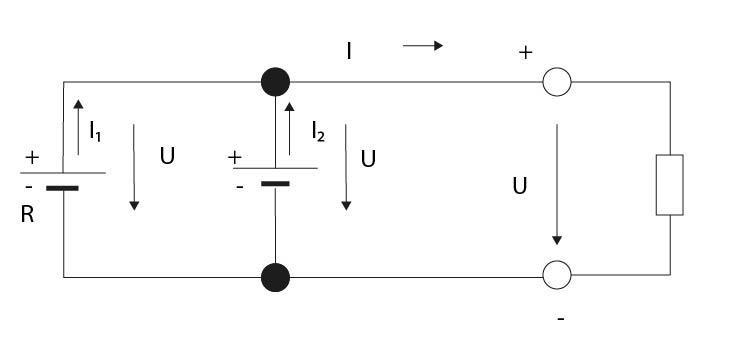
- Jaký proud teče obvodem při řazení zdrojů paralelně:
Na výstupních svorkách se objevuje celkový proud I, který je dán součtem proudů každého z připojených zdrojů.
- Jakén napětí je na výstupních svorkách obvodu při řazení zdrojů se stejným napětím paralelně:
Napětí na výstupních svorkách je stejné, jako napětí na každém z jednotlivých zdrojů, v celém obvodu je kdekoliv pouze toto jediné napětí.
- Výpočet výsledného proudu dvou zdrojů zapojených paralalně:
I= I1 + I2 (A; A, A)
Elektrostatické pole
- Vysvělete pojem elektrostatika:
Elektrostatika se zabývá účinky elektricky nabitých částic či celých těles, které mohou mít náboj souhlasný (např. obě tělesa kladný) a budou se v tomto případě odpuzovat nebo nesouhlasný (jedno těleso bude mít náboj kladný a druhé záporný) a v tomto případě se budou vzájemně přitahovat.
- Vysvětlete pojem Coulombův zákon:
Tento zákon vyjadřuje skutečnost, že síla působící na dvě nabité částice, které se dle polarity svých nábojů budou odpuzovat či přitahovat, je přímo úměrná součinu velikostí jejich nábojů a nepřímo úměrná druhé mocnině jejich vzdálenosti.
- Napište vzorec Coulombova zákona:
`\text {F} = {\text {Q}_1 * \text {Q}_2} / {\text {4} * \text {π} * \ text {ε}_0 * r^2} ` ( N; C,C,F / m,m )
F...síla působící na nabitá tělesa
Q1...velikost náboje prvního tělesa
Q2...velikost náboje druhého tělesa
ε0...dielektrická konstanta (permitivita vakua="8,853 `*` 10-12 F/m
r...vzdálenost těles
- Vysvěltete pojem elektrostatické pole:
Elektrostatické pole je prostor, ve kterém se projevují silové účinky elektrických nábojů, pro lepší představu si ho graficky znázorňujeme pomocí myšlených čar, zvaných elektrické siločáry, které sledují směr silového působení nábojů.
- Vysvětlete pojem elektrostatické pole homogenní:
V homogenním (tedy jiným slovem stejnorodém) elekrostatickém poli jsou elektrické siločáry rovnoběžné, pravidelné, elektrostatické pole je zde konstantní.
- Nakreslete elektrostatické pole homogenní:
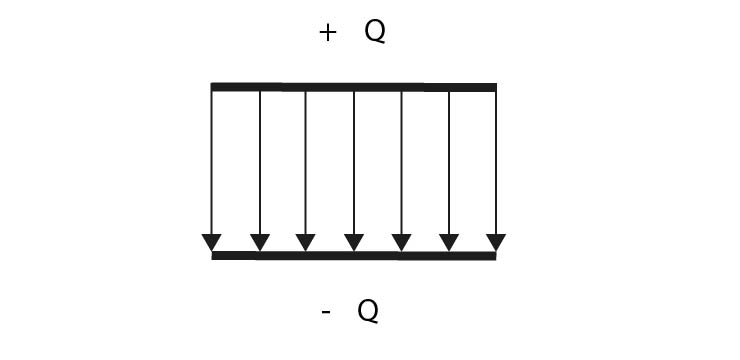
- Vysvětlete pojem elektrostatické pole nehomogenní:
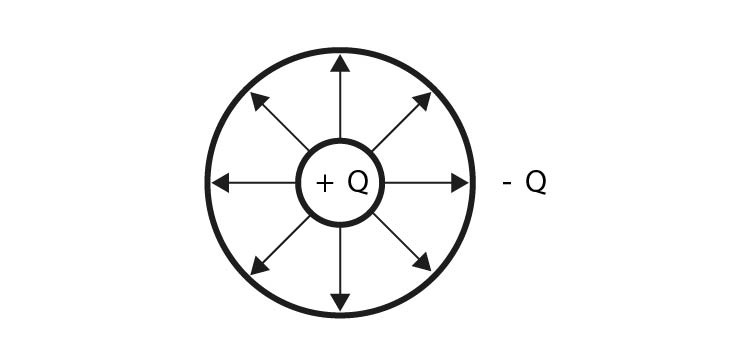
V nehomogenním (tedy jiným slovem nestejnorodém) elekrostatickém poli jsou elektrické siločáry nerovnoběžné, nepravidelné, elektrostatické pole zde není konstantní.
- Nakreslete elektrostatické pole nehomogenní:
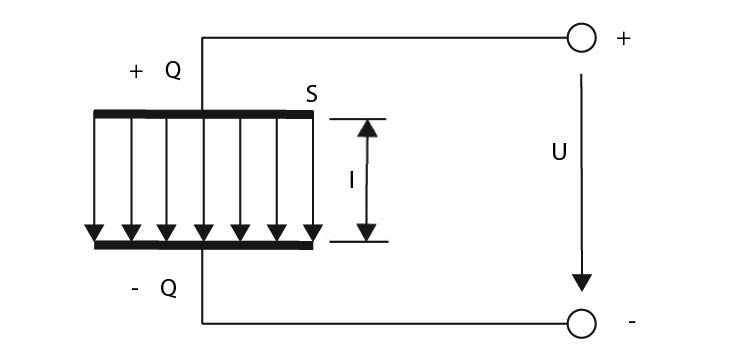
- Vysvětlete pojem kapacita rovinného kondenzátoru:
Rovinný kondenzátor je tvořen dvěma rovnoběžnými kovovými deskami, oddělenými od sebe izolantem zvaným dielektrikum. Jestliže na desky připojíme elektrické napětí, tak se na deskách objeví elektrcké náboje, na jedné desce + Q a na druhé desce - Q. Mezi deskami vznikne homogenní (tedy jiným slovem stejnorodé) elekrostatické pole. Kapacita rovinného kondenzátoru je tedy jeho schopnost hromadit a uchovávat na svých deskách (elektrodách) elektrický náboj.
- Vysvětlete na čem závisí kapacita rovinného kondenzátoru:
Kapacita rovinného kondenzátoru je závislá na ploše elektrod, která se značí S, na vzdálenosti desek čili tloušťce dielektrika, která se značí l, na relativní permitivitě, která se značí εr, na permitivitě vakua, která se značí ε 0. Pojem permitivita vyjadřuje vlastnost daného dielektrika čili izolantu mezi elektrodami (deskami).
- Nakreslete schéma rovinného kondenzátoru:
- Jak se značí kapacita kondenzátoru a jakou má jednotku:
Kapacita rovinného kondenzátoru se značí C a její jednotkou je F (farad). Tato jednotka je dosti velká, proto se v technické praxi také používá jednotek menších:
1 μF= 10-6F
1 nF= 10-9F
1 pF= 10-12F
- Napiště vzorec pro kapacitu rovinného kondenzátoru:
`\text {C} = {\text {ε}_r * \text {ε}_0 * \text {S}} / l ` (F; -,F / m, m2, m)
C...kapacita kondenzátoru
εr...relativní permitivita
ε0...dielektrická konstanta (permitivita vakua= 8,853 `*` 10-12 F/m)
S...plocha desek
l...vzdálenost desek
- Vysvětlete pojem řazení kondenzátorů:
Někdy nám nestačí kapacita jednoho kondenzátoru a proto připojujeme k danému elektrickému kondenzátoru i několik kondenzátorů, které můžeme vzájemně spojovat různým způsobem.
- Vysvětlete pojem řazení kondenzátorů do série:
Tomuto zapojení se také říká zapojení kondenzátorů za sebou a provede se tak, že jeden pól prvního např. elektrolytického kondenzátoru se spojí s opačným pólem druhého elektrolytického kondenzátoru.
- Nakreslete schéma řazení elektrolytických kondenzátorů do série:
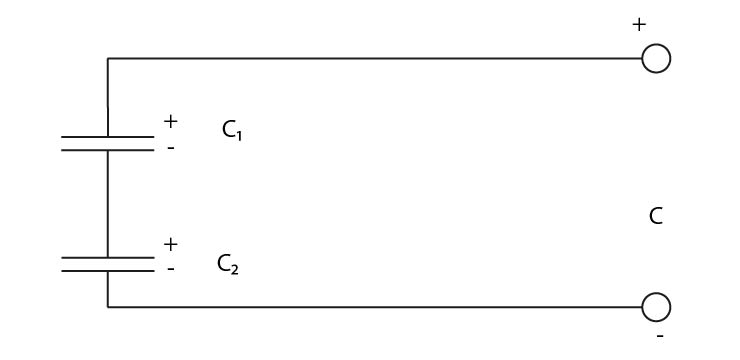
- Výpočet výsledné kapacity dvou kondenzátorů zapojených do série:
`\text {C} = {\text {C}_1 * \text {C}_2} / {\text {C}_1 + \text {C}_2} ` (F; F, F, F, F)
C...celková kapacita kondenzátoru
C1...kapacita prvního kondenzátoru
C2...kapacita druhého kondenzátoru
- Vysvětlete pojem řazení kondenzátorů paralelně:
Tomuto zapojení se také říká zapojení kondenzátorů vedle sebe a provede se tak, že jeden pól prvního např. elektrolytického kondenzátoru se spojí se stejným pólem druhého elektrolytického kondenzátoru.
- Jaké dielektrikum mohou mít kondenzátory:
Mezi kovovými deskami kondenzátoru se nacházejí různé druhy izolantů, např. vzduch, plastická hmota, keramika, slída. U elektrolytických kondenzátorů bývá dielektrikem oxid kovů, záleží zde na polaritě připojeného napětí, jeden pól bývá označen znaménkem plus.
- Nakreslete schema řazení elektolytických kondenzátorů paralelně:
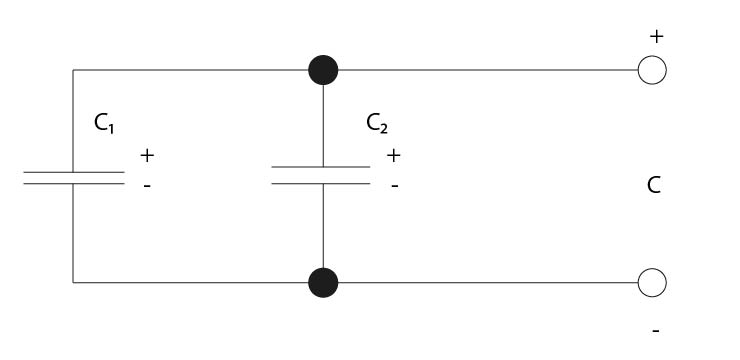
- Výpočet výsledné kapacity dvou kondenzátorů zapojených paralelně:
C= C1 + C2 (F; F, F)
C...celková kapacita kondenzátoru
C1...kapacita prvního kondenzátoru
C2...kapacita druhého kondenzátoru
Elektrochemie
- Vysvětlete, jak působí elektrický proud v kapalinách:
Jestliže vložíme do destilované vody dvě elektrody, připojené na zdroj stejnosměrného proudu, tak zjistíme, že touto vodou neprotéká žádný elektrický proud. Pokud do této vody nasypeme např. chlorid sodný, elektrický proud začne protékat, protože se v ní objevily kladné a záporné ionty.
- Vysvětlete pojem elektrolytická disociace:
Tomuto pojmu lze také říkat rozštěpení, v případě výše uvedeného chloridu sodného tedy rozštěpení na záporně nabité anionty chlóru Cl a kladně nabité kationty sodíku Na.
- Vysvětlete pojem kationt:
Tento pojem znamená, že danému atomu chybí v elektronovém obalu jeden nebo více záporných elektronů, takže navenek se tento atom jeví jako kladný.
- Vysvětlete pojem aniont:
Tento pojem znamená, že daný atom má v elektronovém obalu navíc jeden nebo více záporných elektronů, takže navenek se tento atom jeví jako záporný.
- Vysvětlete vedení elektrického proudu v kapalinách:
Jestliže připojíme na elektrody vložené do roztoku např. chloridu sodného stejnosměrný proud, tak kladně nabité kationty sodíku putují směrem k záporně nabité elektrodě, tedy katodě a záporně nabité anionty chlóru směrem ke kladně nabité elektrodě, tedy k anodě.
- Vysvětlete pojem elektrolyt:
Tímto pojmeme označujeme kapalný vodič, tedy roztok obsahující kladné a záporné ionty.
- Vysvětlete, z čeho je tvořen elektrický proud v kapalinách:
Elektrický proud je zde tvořen kladně nabitými kationty a záporně nabitými anionty nacházejícími se v daném roztoku.
- Vysvětlete pojem elektrochemické zdroje elektrického proudu:
Tyto zdroje umožňují přeměňovat chemickou energii na elektrickou (v případě tzv. suchých článků napájejících např. kapesní svítilnu či MP3 přehrávač) nebo energii chemickou na elektrickou při vybíjení a elektrickou na chemickou při nabíjení (v případě akumulátorů např. do automobilů či mobilních telefonů).
- Vysvětlete pojem elektrický akumulátor:
Umožňuje opakovanou přeměnu energie elektrické na chemickou energii a naopak.
- Jaké znáte druhy akumulátorů:
Nejčastěji se lze setkat s akumulátory např. olověnými Pb, oceloniklovými NiFe, niklokadmiovými NiCd.
Magnetismus a lektromagnetismus
- Vysvětlete pojem magnetické pole:
Magnetické pole je prostor, ve kterém se projevují silové účinky magnetu.
- Jak znázorňujeme magnetické pole:
Pro lepší představu si ho graficky znázorňujeme pomocí myšlených čar zvaných magnetické indukční čáry (nebo také magnetické siločáry), které sledují směr od severního pólu S k jižnímu pólu J.
- Vysvětlete pojem magnetické pole homogenní:
V homogenním (tedy jiným slovem stejnorodém) magnetickém poli jsou magnetické siločáry rozmístěny rovnoběžné, pravidelné, magnetické pole je zde konstantní.
- Nakreslete magnetické pole homogenní:
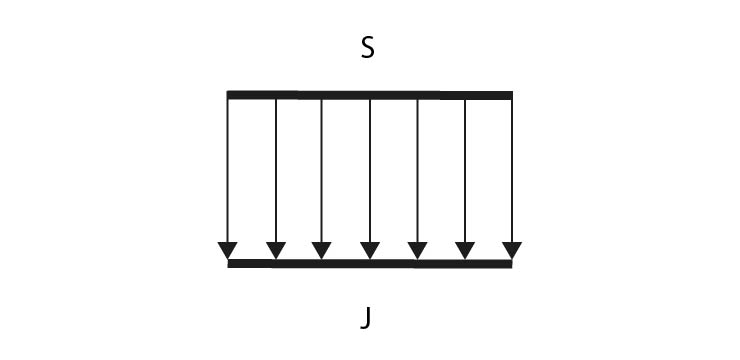
- Vysvětlete pojem magnetické pole nehomogenní:
V nehomogenním (tedy jiným slovem nestejnorodém) magnetickém poli jsou magnetické siločáry nerovnoběžné, nepravidelné, magnetické pole zde není konstantní.
- Nakreslete magnetické pole nehomogenní:
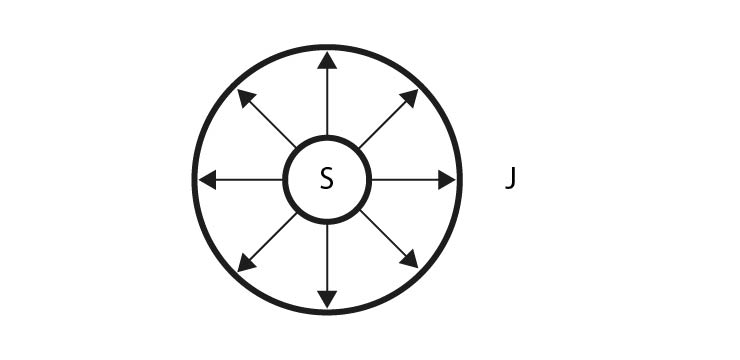
- Vysvětlete pojem látky magnetické a nemagnetické:
Látky, které považujeme za nemagnetické, se dělí na diamagnetické ( jsou po vložení do magnetického pole tímto polem slabě vypuzovány ) a paramagnetické (jsou po vložení do magnetického pole tímto polem slabě vtahovány ). Látky magnetické se nazývají feromagnetické (jsou po vložení do magnetického pole tímto polem silně vtahovány a tzv. magnetováním z nich vznikají magnety).
- Vysvětlete princip magnetismu:
Látky jsou složeny z atomů, kolem jejich jádra obíhají po uzavřených drahách elektrony , kterým je připisována ještě další vlastnost, a to otáčení kolem své vlastní osy, tzv. spin, který pokládáme za příčinu magnetických vlastností látek.
- Vysvětlete pojem elektromagnetismus:
Jestliže jsou magnetické vlastnosti látek vyvolány průchodem elektrického proudu těmito látkami, hovoříme o elektromagnetismu.
- Vysvětlete pojem magnetické pole vodiče:
Přiložíme-li k vodiči protékanému elektrickým proudem magnetku, zjistíme, že tato se vychýlí, jakoby byl vodič magnetem. Z toho vyplývá, že kolem vodiče vzniká průchodem elektrického proudu magnetické pole.



- Vysvětlete pojem magnetické pole cívky:
Cívka vzniká navinutím původně rovného vodiče na kostru z izolantu mající tvar válce a průchodem elektrického proudu závity takto vzniklé cívky vzniká její magnetické pole, o kterém se rovněž můžeme přesvědčit přiloženou magnetkou. Ta se vychýlí, jakoby cívka byla magnetem.




- Vysvětlete pojem elektromagnet:
Elektromagnetem se stává jakákoliv cívka, kterou v daném okamžiku protéká elektrický proud, na jednom jejím konci se vytváří severní a na druhém konci jižní pól.
- Vyjmenujte nejčastější magnetické veličiny a jednotky:
Magnetická indukce se značí B a má jednotku 1 T (tesla)
Magnetický tok se značí Φ a má jednotku 1 Wb (weber)
Intenzita magnetického pole se značí H a má jednotku 1 A/m (ampér na metr)
Magnetický odpor se značí R m a má jednotku 1/ H (jedna lomeno henry)
Magnetická vodivost se značí G ma má jednotku 1 H (henry)
Magnetické napětí se značí U m a má jednotku 1 A (ampér)
Počet závitů cívky se značí N a nemá žádnou jednotku
Střední délka magnetická indukční čáry se značí ls a má jednotku 1m (metr)
Relativní permeabilita se značí µ r a nemá žádnou jednotku
Permeabilita vakua se značí µ 0 a má jednotku 1 H/m (henry na metr)
- Vysvětlete pojem Hopkinsonův zákon:
Je obdobou Ohmova zákona a má tento tvar
`\text {R}_m = \text {U}_m / \text{Φ}` (1/ H; A, Wb)
Rm...magnetický odpor
Um...magnetické napětí
Φ...magnetický tok
- Co vzniká pohybem vodiče a cívky v magnetickém poli:
Tím, že pohybem vodiče či cívky v magnetickém poli protínáme jeho magnetické siločáry, dochází k indukování elektrického napětí, měřitelného na koncích vodiče či cívky.
- Vysvětlete pojem elektrodynamické účinky proudu:
Jsou-li dva rovnoběžné vodiče protékány elektrickým proudem, vzniká kolem každého z nich jeho magnetické pole, tato pole na sebe vzájemně působí a oba vodiče na sebe působí silami, které podle směru proudů ve vodičích je k sobě přitahují či od sebe odpuzují.
- Vysvětlete pojem elektromagnetická indukce:
Vložíme-li vodič do magnetického pole, objeví se při každé změně tohoto pole na koncích tohoto vodiče napětí, kterému říkáme indukované napětí.
- Vysvětlete pojem vznik proudu ve vodiči:
Budeme-li pohybovat vodičem v magnetickém poli kolmo k indukčním čarám, bude se v něm indukovat elektrické napětí.
- Uveďte vzorec pro výpočet napětí indukovaného ve vodiči:
U= B `*` l `*` v (V; T, m, m/s)
U...elektrické napětí
B...magnetická indukce
l...délka vodiče, která zasahuje do magnetického pole
v...rychlost pohybu vodiče v magnetickém polic
- Uveďte pravidlo pravé ruky pro směr magnetického pole ve vodiči:
Uchopíme-li vodič do pravé ruky tak, aby vychýlený palec ukazoval směr proudu, potom prsty, objímající vodič, ukazují směr působení magnetického pole.
- Uveďte pravidlo pravé ruky pro směr magnetického pole v cívce:
Uchopíme-li cívku do pravé ruky tak, aby prsty ukazovaly směr proudu, potom vychýlený palec ukazuje směr indukčních čar a severní pól cívky.
- Uveďte pravidlo pravé ruky pro směr indukovaného proudu ve vodiči:
Pravou ruku držíme tak, aby siločáry vstupovaly do dlaně a natažený palec ukazoval směr pohybu vodiče, potom prsty ukazují směr indukovaného proudu.
- Uveďte pravidlo levé ruky pro vychýlení vodiče:
Siločáry vstupují do daně, prsty ukazují směr proudu, vychýlený palec ukazuje směr vychýlení vodiče.
Střídavé proudy
- Vysvětlete pojem vznik střídavého sinusového napětí:
Jestliže budeme otáčet závitem vodiče v magnetickém poli, bude se ve vodiči indukovat střídavé napětí sinusového průběhu.
- Vysvětlete, na čem závisí kmitočet vzniklého střídavého sinusového napětí:
Kmitočet indukovaného střídavé napětí sinusového průběhu závisí na otáčkách závitu vodiče v magnetickém poli a na počtu pólových dvojic magnetů, mezi kterými se závit otáčí.
- Vysvětlete, jak se chová rezistor v obvodu střídavého proudu:
Proud procházející rezistorem je ve fázi s napětím na rezistoru.
- Vysvětlete, jak se chová cívka v obvodu střídavého proudu:
Napětí na cívce předbíhá o 90 stupňů před proudem procházejícím cívkou.
- Vysvětlete, jak se chová kondenzátor v obvodu střídavého proudu:
Proud kondenzátoru předbíhá o 90 stupňů před napětím na kondenzátoru.
- Vysvětlete, jakých hodnot může dosahovat střídavé sinusové napětí nebo proud:
Střídavý proud nebo napětí mají v každém časovém okamžiku jinou velikost a proto u nich rozeznáváme :
okamžité hodnoty – odpovídají určitému okamžiku, značí se malými písmeny i, u,
maximální hodnoty – jsou největší okamžité hodnoty, značí se velkými písmeny Imax, Umax,
efektivní hodnoty – jsou nejužívanější, značí se velkými písmeny I, U
střední hodnoty – mají význam u usměrňovačů, značí se velkými písmeny Istř, Ustř
- Vysvětlete pojem efektivní hodnota střídavého sinusového proudu:
Efektivní hodnota střídavého proudu odpovídá stejné hodnotě stejnosměrného proudu, který v rezistoru za stejnou dobu vyvolá stejné tepelné účinky jako uvažovaný střídavý proud.
- Vysvětlete pojem kmit:
Kmit u sinusového průběhu se skládá z kladné a záporné půlvlny.
- Vysvětlete pojem kmitočet:
Kmitočet se značí f, má jednotku 1Hz (hertz), udává počet kmitů za 1 sekundu.
- Vysvětlete pojem doba kmitu:
Doba kmitu se značí T , má jednotku 1s (sekunda), udává dobu, za kterou se vykoná jeden celý sinusový kmit.
- Jak se vypočítá doba kmitu z kmitočtu:
`\text {T} = \text {1} / \text{f}` (s;-, Hz)
T...doba kmitu
f...kmitočet
- Jak se vypočítá kmitočet z doby kmitu:
`\text {f} = \text {1} / \text{T}` (Hz, -, s)
f...kmitočet
T...doba kmitu
- Jak se vypočítá maximální hodnota napětí z efektivní hodnoty napětí:
Umax= 1,414 `*` U (V, -, V)
Umax...maximální hodnota napětí
U...efektivní hodnota napětí
- Jak se vypočítá maximální hodnota proudu z efektivní hodnoty proudu:
I max= 1,414 `*` I (A, -, A)
Imax...maximální hodnota proudu
I...efektivní hodnota proudu
- Jak se vypočítá efektivní hodnota napětí z maximální hodnoty napětí:
U= 0,707 `*` Umax (V, -, V)
U...efektivní hodnota napětí
Umax...maximální hodnota napětí
- Jak se vypočítá efektivní hodnota proudu z maximální hodnoty proudu:
I= 0,707 `*` Imax (A, -, A)
I...efektivní hodnota proudu
Imax...maximální hodnota proudu
- Jak se vypočítá střední hodnota napětí z maximální hodnoty napětí:
U stř= 0,637 `*` U max (V, -, V)
Ustř...střední hodnota napětí
Umax...maximální hodnota napětí
- Jak se vypočítá střední hodnota proudu z maximální hodnoty proudu:
Istř= 0,637 `*` Imax (A, -, A)
Istř...střední hodnota proudu
Imax...maximální hodnota proudu
- Vysvětlete pojem ohmické zatížení:
Do střídavého obvodu je zapojen jako spotřebič rezistor s hodnotou odporu vyjádřenou např.v ohmech.
- Vysvětlete pojem indukčnost vlastní:
Průchodem střídavého proudu cívkou se v ní budí proměnný magnetický tok, v důsledku čehož se indukuje v cívce indukční elektrické napětí. Schopnost cívky budit vlastním magnetickým tokem svoje indukované napětí se nazývá vlastní indukčnost.
- Jak se značí indukčnost vlastní a jakou má jednotku:
Vlastní indukčnost se značí L a má jednotku 1 H (henry).
- Kdy má cívka indukčnost 1 henry:
Cívka, kterou prochází střídavý elektrický proud, má indukčnost jednoho henry, jestliže se v ní indukuje elektrické napětí jednoho voltu při rovnoměrné změně proudu jeden ampér za jednu sekundu.
- Vysvětlete pojem indukční odpor:
Cívka, kterou prochází střídavý proud, klade jeho průchodu určitou překážku, které říkáme indukční odpor.
- Jak se značí indukční odpor a jakou má jednotku:
Indukční odpor se značí XL a má jednotku 1 Ω (ohm). Říká se jí také induktivní reaktance.
- Jak se vypočítá indukční odpor:
XL= 2 `*` π `*` f `*` L ( Ω; -, -, Hz, H )
XL...indukční odpor
f...kmitočet
L...indukčnost cívky
Nebo z Ohmova zákona platí vztah:
`\text {X}_L = \text {U} / \text{I}` ( Ω; V, A )
XL...indukční odpor
U...elektrické napětí
I...elektrický proud
- Jak se značí indukční vodivost a jakou má jednotku:
Indukční vodivost se značí BL a má jednotku 1 S (siemens). Říká se jí také induktivní susceptance.
- Jak se vypočítá indukční vodivost:
`\text {B}_L = \text {1} / \text{X}_L` (S; -, Ω)
BL...indukční vodivost
XL...indukční reaktance
- Vysvětlete pojem kapacitní odpor:
Kondenzátor, kterým prochází střídavý proud, klade jeho průchodu určitou překážku, které říkáme kapacitní odpor.
- Jak se značí kapacitní odpor a jakou má jednotku:
Kapacitní odpor se značí Xc a má jednotku 1 Ω (ohm). Říká se jí také kapacitní reaktance.
- Jak se vypočítá kapacitní odpor:
`\text {X}_c = \text {1} / {\text{2} * \text {π} * \text {f} * \text{C}}` ( Ω; -, -, -, Hz, F )
XC... kapacitní reaktance
f... kmitočet
C... kapacita kondenzátoru
Nebo z Ohmova zákona platí vztah:
`\text {X}_c = \text {U} / {\text{I}` ( Ω; V, A )
XC...kapacitní reaktance
U... elektrické napětí
I... elektrický proud
- Jak se značí kapacitní vodivost a jakou má jednotku:
Kapacitní vodivost se značí BC a má jednotku 1 S (siemens). Říká se jí také kapacitní susceptance.
- Jak se vypočítá kapacitní vodivost:
`\text {B}_C = \text {1} / {\text{X}_C} ` ( S; -, Ω )
BC... kapacitní vodivost
XC... kapacitní reaktance
- Vysvětlete pojem obecná impedance:
Tímto pojmem rozumíme celkový zdánlivý odpor jedné nebo více součástek zapojených do střídavého elektrického obvodu.
- Jak se značí obecná impedance a jakou má jednotku:
Obecná impedance se značí Z a má jednotku 1 Ω (ohm). Říká se jí také jinými slovy zdánlivý odpor.
- Jak se vypočítá obecná impedance:
Z Ohmova zákona platí vztah
`\text {Z} = \text {U} / \text{I} ` ( Ω; V, A )
Z... impedance
U... elektrické napětí
I...elektrický proud
- Vysvětlete pojem obecná admitance:
Tímto pojmem rozumíme celkovou zdánlivou vodivost jedné nebo více součástek zapojených do střídavého elektrického obvodu.
- Jak se značí obecná admitance a jakou má jednotku:
Obecná admitance se značí Y a má jednotku 1 S (siemens). Říká se jí také jinými slovy zdánlivá vodivost.
- Jak se vypočítá obecná admitance:
Obecná admitance Y je rovna převrácené hodnotě impedance Z:
`\text {Y} = \text {1} / \text{Z}` ( S; -, Ω )
Y...admitance
Z...impedance
- Vysvětlete pojem rezonanční obvod:
Je to střídavý elektrický obvod složený z rezistoru, cívky, kondenzátoru, ve kterém nastává při určitém kmitočtu stav, kdy indukční reaktance cívky a kapacitní reaktance kondenzátoru jsou stejně velké a navzájem se ruší. Při rezonanci dochází k výměně energie mezi magnetickým polem cívky a elektrickým polem kondenzátoru.
- Vysvětlete pojem sériový rezonanční obvod:
Tento obvod je složen ze seriového zapojení rezistoru, cívky, kondenzátoru. Při určitém kmitočtu jsou napětí cívky a napětí kondenzátoru stejně velké, jejich rozdíl je nulový. Napětí na cívce a napětí kondenzátoru může dosáhnout nebezpečné několikrát vyšší hodnoty než napětí na napájecích svorkách obvodu. Při seriové rezonanci protéká obvodem maximální proud, omezený jen velikostí ohmického odporu rezistoru.
- Vysvětlete pojem paralelní rezonanční obvod:
Tento obvod je složen z paralelního zapojení rezistoru, cívky, kondenzátoru. Při určitém kmitočtu jsou proud cívky a proud kondenzátoru stejně velké, jejich rozdíl je nulový. Proud v obvodu může dosáhnout nebezpečné několikrát vyšší hodnoty. Při paralelní rezonanci protéká obvodem minimální proud, omezený jen velikostí impedance, napětí obvodu je při rezonanci maximální.
- Vysvětlete pojem Thomsonův vzorec:
Tento vzorec umožňuje výpočet rezonančního kmitočtu paralelního i seriového rezonančního obvodu z hodnot použitých součástek v obvodu.
- Uveďte Thomsonův vzorec:
`\text {f} = \text {1} / {\text{2} * \text {π} * \text \sqrt{\ L * \ C}}` (Hz,; -, -, -, H, F)
f...kmitočet
L...indukčnost cívky
C...kapacita kondenzátoru
- Vysvětlete se cos φ a je dán podílem činného výkonu P a zdánlivého výkonu S a nemá žádnou jednotku
`\text {cos φ} = \text {P} / \text{S} ` (-; W, VA)
cos φ...účiník
P...činný výkon
S...zdánlivý výkon
- Uveďte vztah pro jednofázový činný výkon:
P = U `*` I `*` cos φ (W; V, A, -)
P...činný výkon
U...elektrické napětí
I...elektrický proud
cos φ...účiník
- Uveďte vztah pro jednofázový jalový výkon:
Q = U `*` I `*` sin φ (VAr; V, A, -)
Q...jalový výkon
U...elektrické napětí
I...elektrický proud
sin φ...sinus fázového úhlu φ
- Uveďte vztah pro jednofázový zdánlivý výkon:
S = U `*` I (VA; V, A, -)
S...zdánlivý výkon
U...elektrické napětí
I...elektrický proud
- Uveďte vztah pro jednofázovou práci:
A = U `*` I `*` cos φ `*` t (J; V, A, -, s)
A...elektrická práce
U...elektrické napětí
I...elektrický proud
cos φ...účiník
t...čas
- Uveďte vztah pro třífázový činný výkon:
P = √ 3 `*` U `*` I cos φ (W; -, V, A, -)
P...činný výkon
U..sdružené elektrické napětí
I...sdružený elektrický proud
cos φ...účiník
- Uveďte vztah pro třífázový jalový výkon:
Q = √ 3 `*` U `*` I `*` sin φ (VAr; -, V, A, -)
Q...jalový výkon
U...sdružené elektrické napětí
I...sdružený elektrický proud
sin φ...sinus fázového úhlu φ
- Uveďte vztah pro třífázový zdánlivý výkon:
S = √ 3 `*` U `*` I (VA; -, V, A, -)
U...sdružené elektrické napětí
I...sdružený elektrický proud
- Uveďte vztah pro třífázovou práci:
A = √ 3 `*` U `*` I `*` cos φ `*` t (J; -, V, A, -,s)
A...elektrická práce
U...sdružené elektrické napětí
I...sdružený elektrický proud
cos φ...účiník
t...čas
- Vysvětlete vznik třífázového proudu:
Tento druh proudu se vyrábí v alternátoru, který má soustavu tří cívek navzájem pootočených o 120 stupňů. Z každé cívky je vyvedena tzv. fáze. Na cívky působí otočné magnetické pole, které v nich indukuje napětí. Tato napětí mají sinusový průběh a jsou časově posunutá o 120 stupňů.
- Vysvětlete pojem spojení vinutí do hvězdy:
Začátky všech tří cívek vinutí jsou zapojeny do uzlu, ze kterého je vyveden střední (neutrální) vodič, konce cívek jsou vyvedeny na svorky jednotlivých fází. Mezi kteroukoli fází a středním vodičem je tzv. fázové napětí, které v běžné střídavé rozvodné síti má jmenovitou hodnotu 230 V. Mezi kterýmikoli dvěma fázemi je tzv. sdružené napětí, které v běžné střídavé rozvodné síti má jmenovitou hodnotu 400 V.
Sdružené napětí je √ 3 krát větší než fázové napětí.
- Vysvětlete pojem spojení vinutí do trojúhelníka:
U tohoto zapojení je vždy spojen konec jedné cívky se začátkem druhé cívky, není zde vyveden žádný střední (neutrální) vodič. Je zde pouze jeden druh napětí a to fázové, které se zde rovná napětí sdruženému.