Pojem souřadný systém známe z geometrie. V praxi jej využíváme napříč různými odvětvími v průmyslu, stavebnictví, vojenství ale i v lékařství… na jeho principu funguje celá řada pro lidstvo důležitých vynálezů, od navigace a konstrukce až po zobrazování grafiky a digitální fotografii. Souřadný systém lze v zásadě rozdělit na Kartézský a Polární. Oba jsou na světě již velmi dlouhou dobu.
Kartézský souřadný systém
Jako první jej matematicky popsal a také patentoval René Descartes (*31. 3. 1596 - †11. 2. 1650) francouzský filosof, matematik a fyzik. Název systému je tedy odvozen z latinského překladu jeho příjmení Cartesius. Soustava dvou nebo tří os vzájemně se protínajících v nule dokáže definovat bod v ploše či prostoru za pomoci milimetrových stupnic (podobně jako na školním pravítku) nanesených na jednotlivých osách.
|
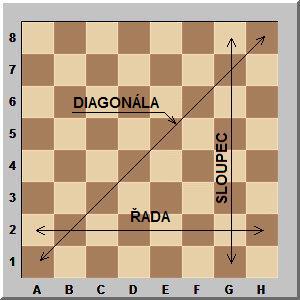
Způsob pohybu některých figur v šachové hře (např. dámy) připomíná pohyb nástroje do cílové souřadnice - pohyb po přímce. Hru je možné pomocí výpisu výchozích a cílových polí jednotlivých figur celou zaznamenat. Vznikne tak vlastně jednoduchý "program" konkrétní hry. |
Obr. 1
|
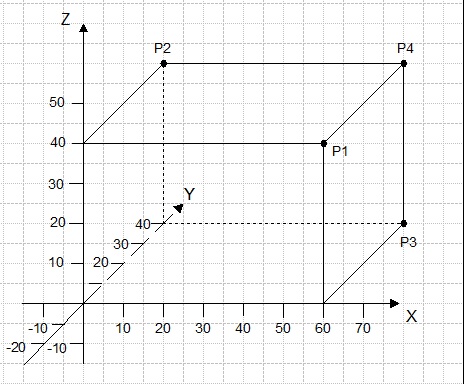
Kartézský pohyb ve třech osách s příkladem cílových souřadnic. Příklad:
|
Obr. 2
|
Kartézský souřadný systém vyjádřený čtyřmi tzv. "kvadranty" kde první je vždy kladný, třetí vždy záporný a další dva kvadranty jsou tzv. přechodné tj. jedna z os je má hodnotu kladnou a druhá zápornou. Tato pravidla je třeba dodržovat i při programování. |
Obr. 3

Polární Souřadný systém
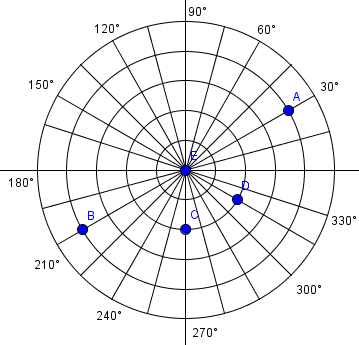
Polární systém souřadnic je dvoudimenzionální systém souřadnic (pracuje tedy pouze v jedné rovině), ve kterém je každý bod určen úhlem a vzdáleností viz. příklad absolutního zadání.
|
Bod A [4, 30°] Bod B [4, 210°] Bod C [2, 270°] Bod D [2, 315°] Bod E [0, 0°] |
Obr. 4
|
Centrálním bodem soustavy je tedy pól (střed) a rovina, od které odečítáme
úhel, můžeme si ji představit jako hladinu vody (kartézsky vodorovná osa
X). Existuje opět ve dvou polaritách a to v kladné levotočivé a záporné
pravotočivé. Každý úhel lze tedy vyjádřit ve dvou variantách.
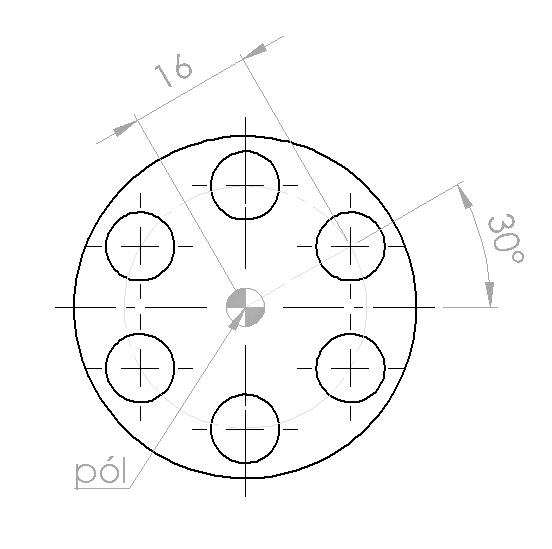
V praxi jej používáme především tam, kde pracujeme s úhlovými hodnotami nebo s rádiusovými tvary. Jako příklad nám může posloužit bubínek revolveru. Souřadnice vrtaných otvorů lze samozřejmě určit i kartézsky, polární zadání je však pro tento případ mnohem snáze použitelné. Šest otvorů umístněných na roztečné kružnici s poloměrem R=16 má úhlovou vzdálenost 60° (tedy 360°: 6) Úhel 30° určuje pozici prvního z otvorů vůči pólu. |
Obr. 5