Vysvětlení konstrukčního použití a formy zápisu kontury u složitějších a neúplně zakótovaných kontur, odvozování pozic cílových bodů z již hotové kontury, použití širší možnosti zápisu - "všechny parametry" formou kartézského i polárního zápisu.
Obr. 290
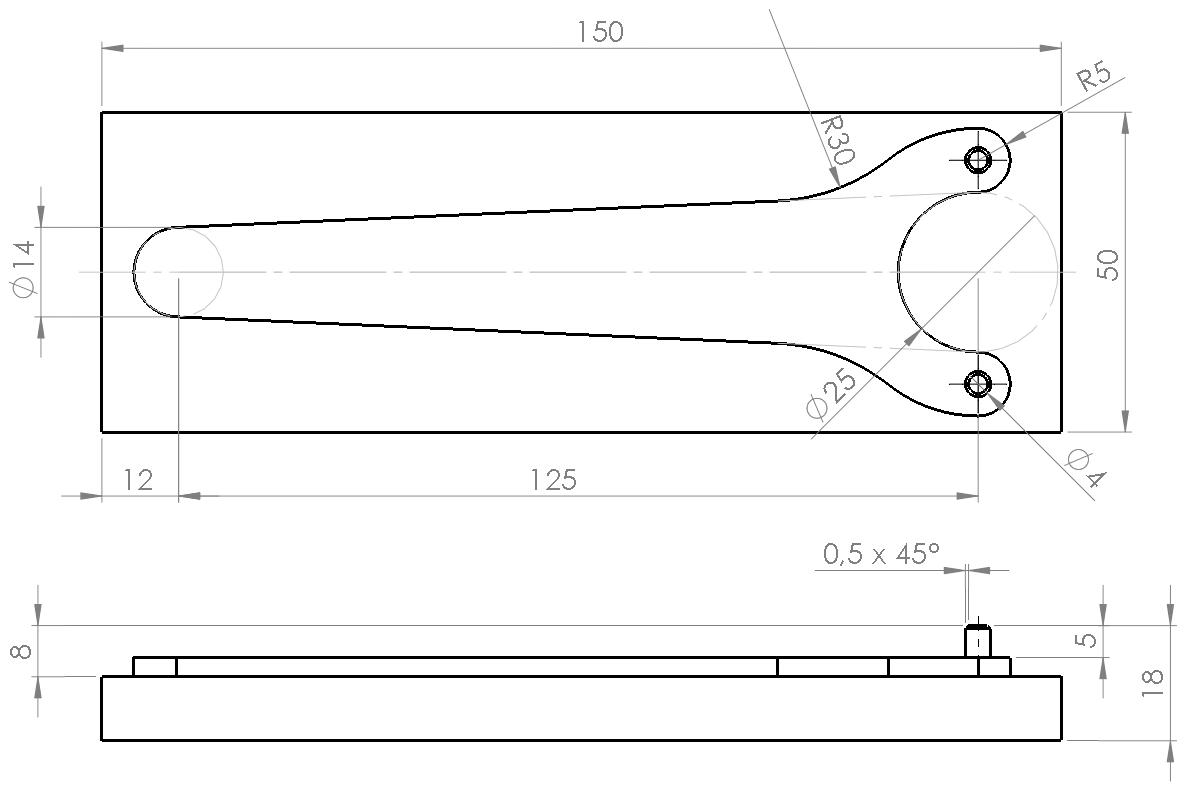
V dílenské praxi se občas setkáme s případy neúplně zakótovaných výkresů. Někdy chybí úhel, jindy délka entity, případně roztečná kružnice. Rozměry si nemůžeme vymýšlet, a tak nám nezbývá, než dokumentaci vrátit k přepracování. Případně, máme-li k dispozici výchozí model těleso dokótovat. Vychází-li však rozměry z některých geometrických vlastností, může nám být grafický editor významným pomocníkem. Na výše uvedeném příkladu si tyto možnosti ukážeme. Konturu kreslíme vždy z místa, které je jednoznačně určené a pokud možno, dobře přístupné pro nájezd nástroje.
Obr. 291
Obr. 292
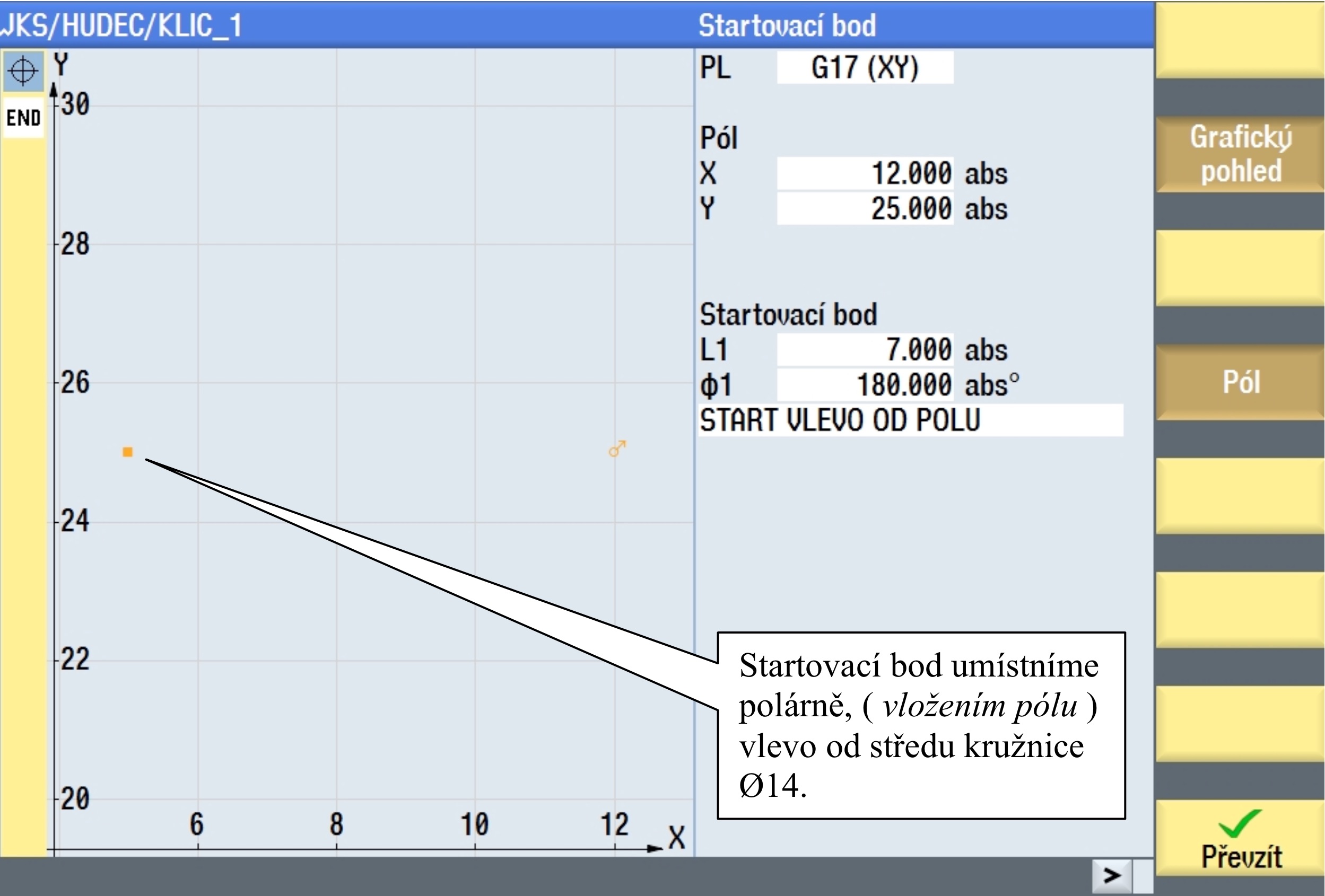
Vzhledem k tomu, že kružnice bude na základě tečnosti oříznuta následující entitou, nesnažíme se zadat její cílový bod. Prostě jej neznáme a tak použijeme pouze její střed.
Obr. 293
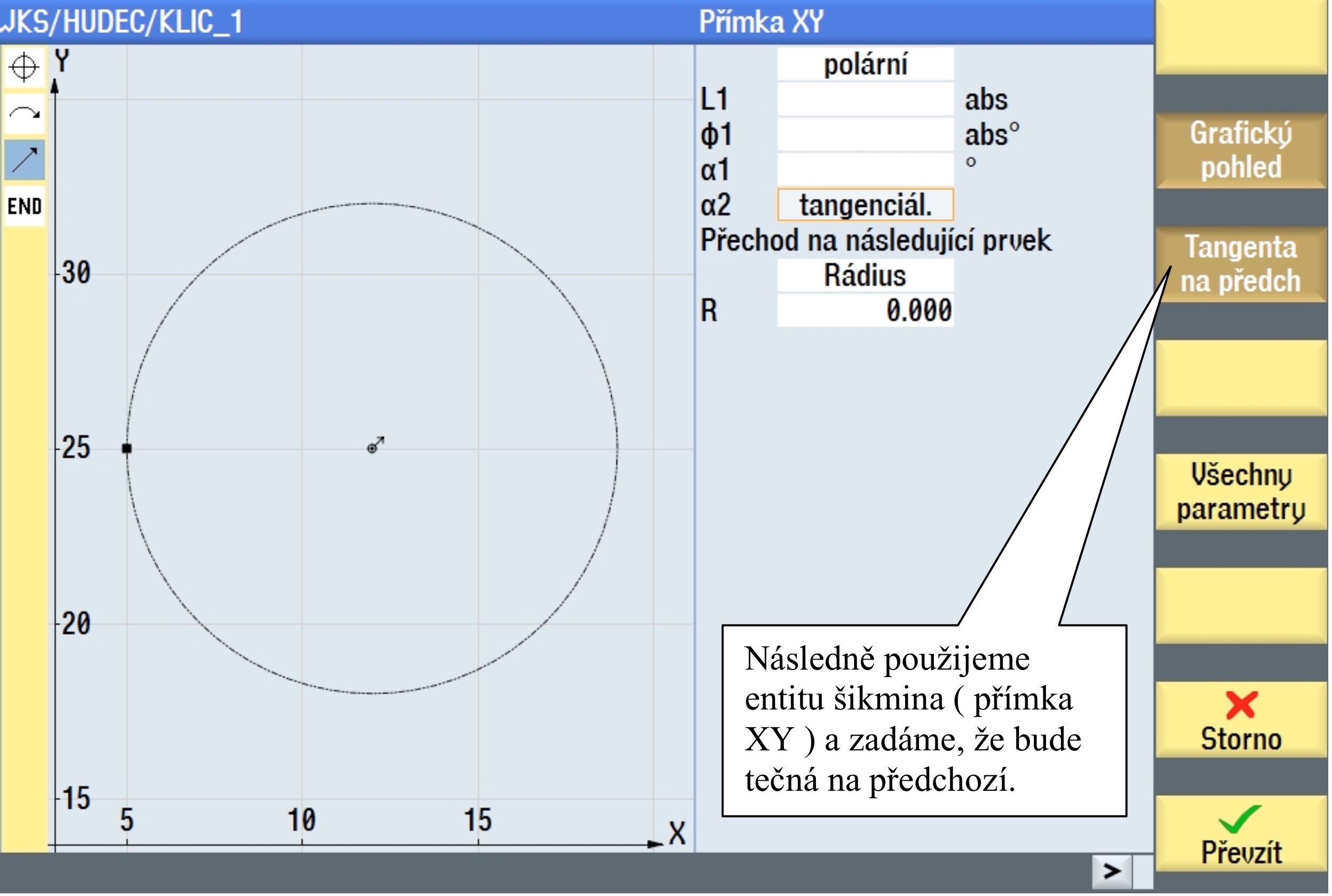
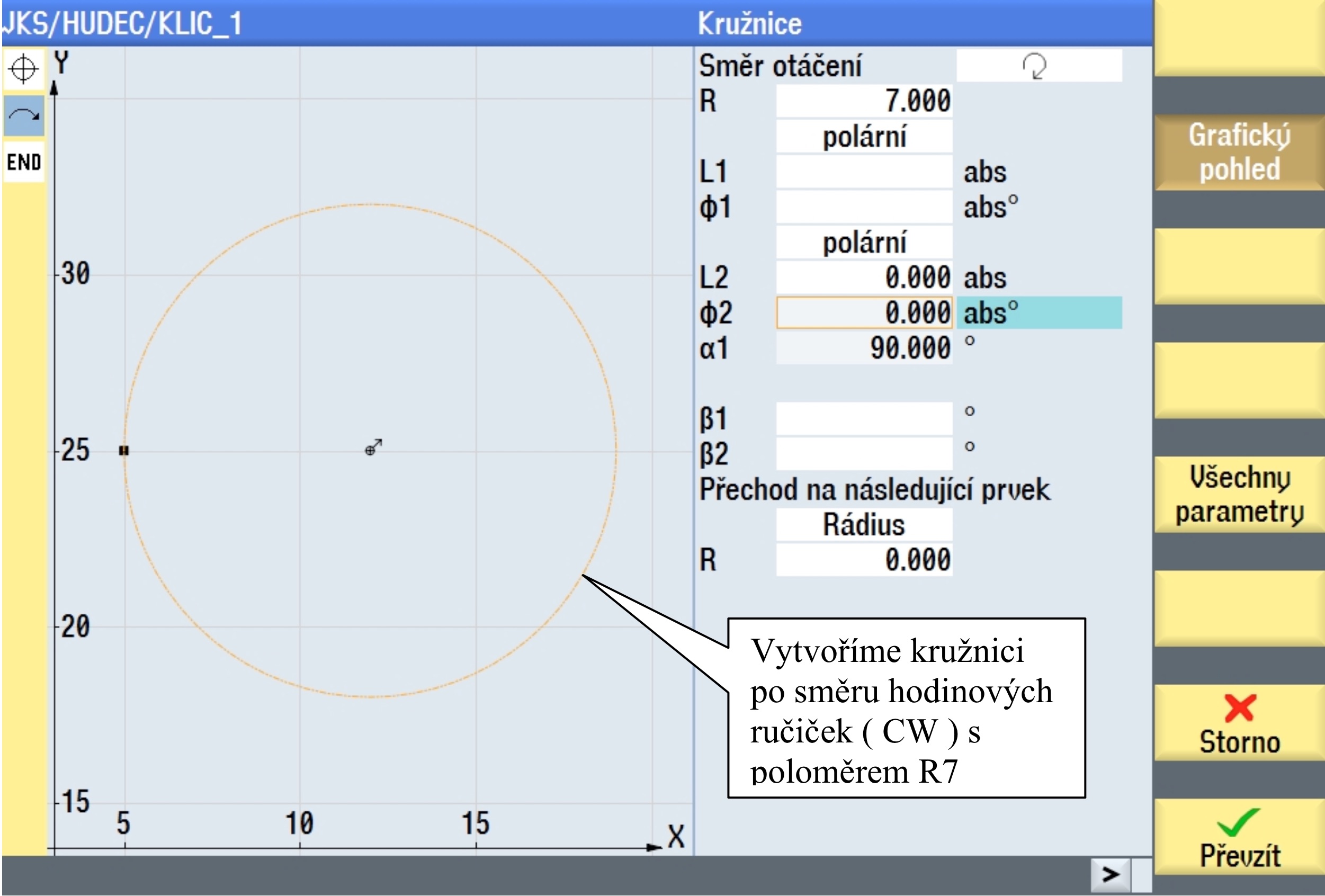
Napojením na kružnici s průměrem 25 mm, docílíme správného zapolohování naší šikminy. Úhel α1 si opíšeme pro další použití v konstrukci. Následně vazbu zrušíme, smazáním prvku kružnice červeným křížkem "Storno". Nebo, pokud jste již převzali, klávesou "Smazat prvek".
Obr. 294
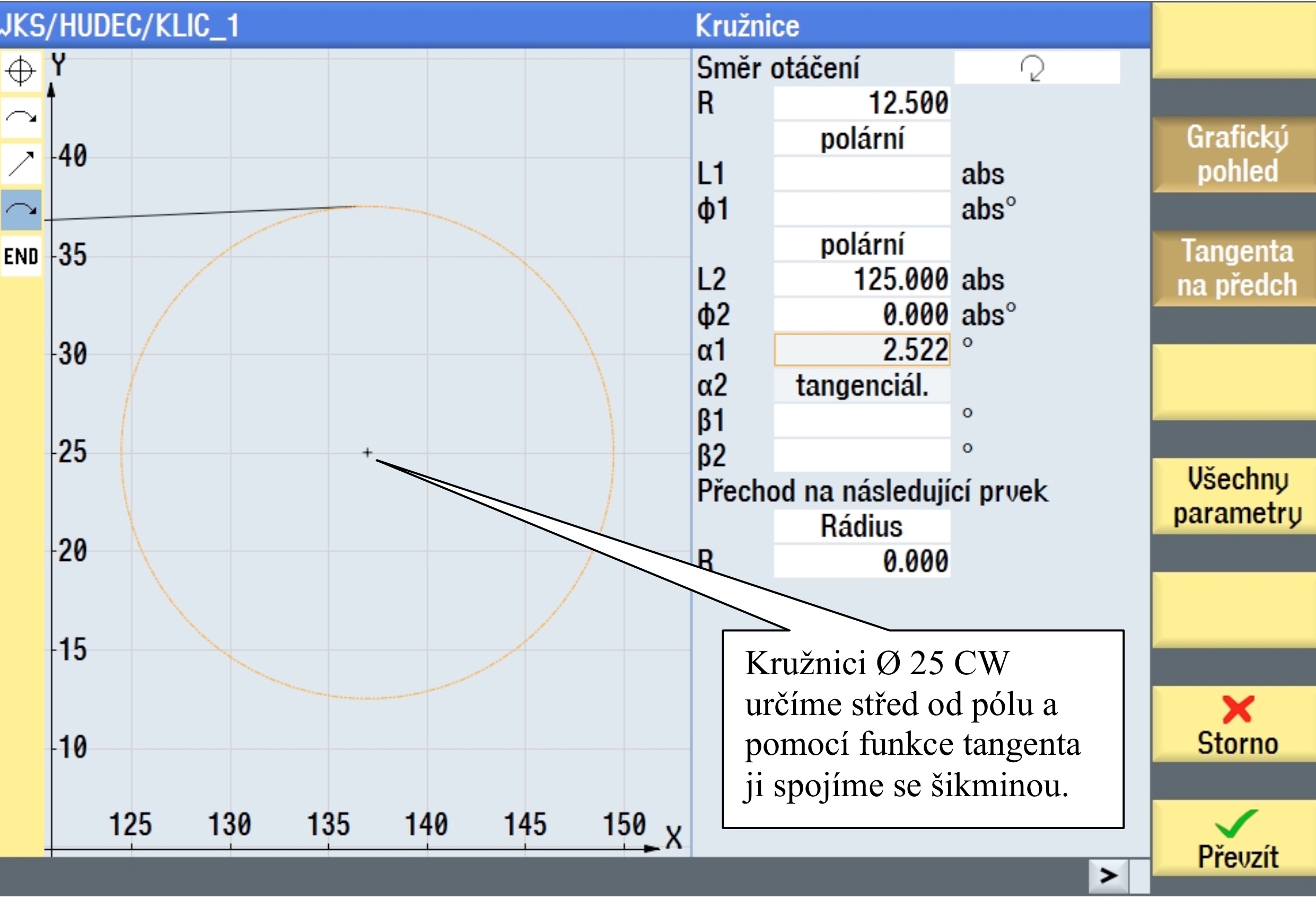
Pokračovat budeme jinou kružnicí ( ze stejného středu ), jejíž poloměr odvodíme od poloměrů R5 obou ramen klíče. Nejprve se však vrátíme na entitu šikminy a doplníme úhel α1 = 2.522°.
Po oříznutí kružnicí R 22.5 CW vybereme v dialogovém okně správné řešení a převezmeme.
Obr. 295
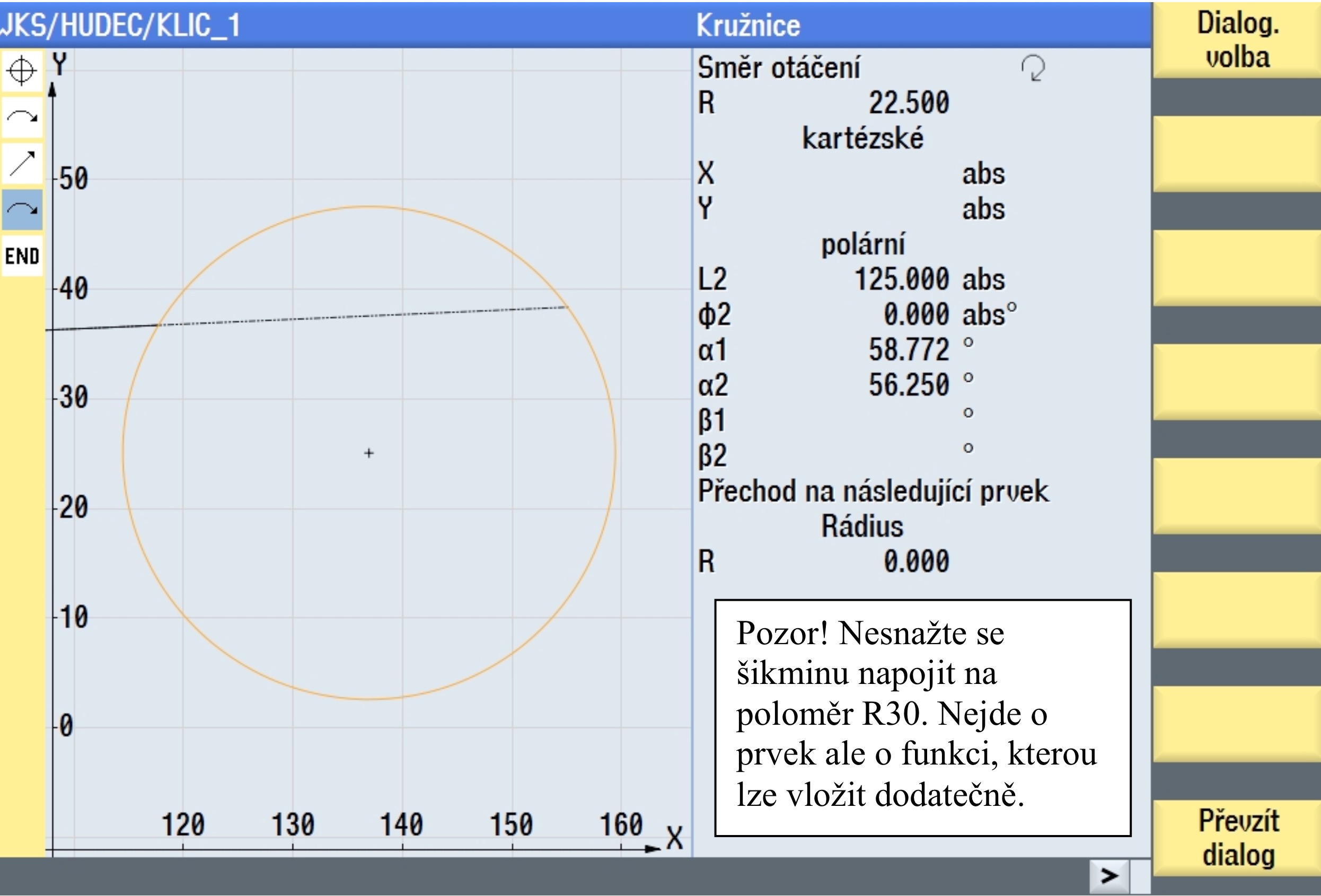
Po správném převzetí dialogu ( oříznutí šikminy kružnicí ), by situace měla vypadat takto. Za pomoci tečné vazby jsme zkonstruovali pomocné napojení a vyšetřili tak chybějící úhel šikminy, která je následně oříznuta jinou kružnicí ( R22.5 ).
Obr. 296
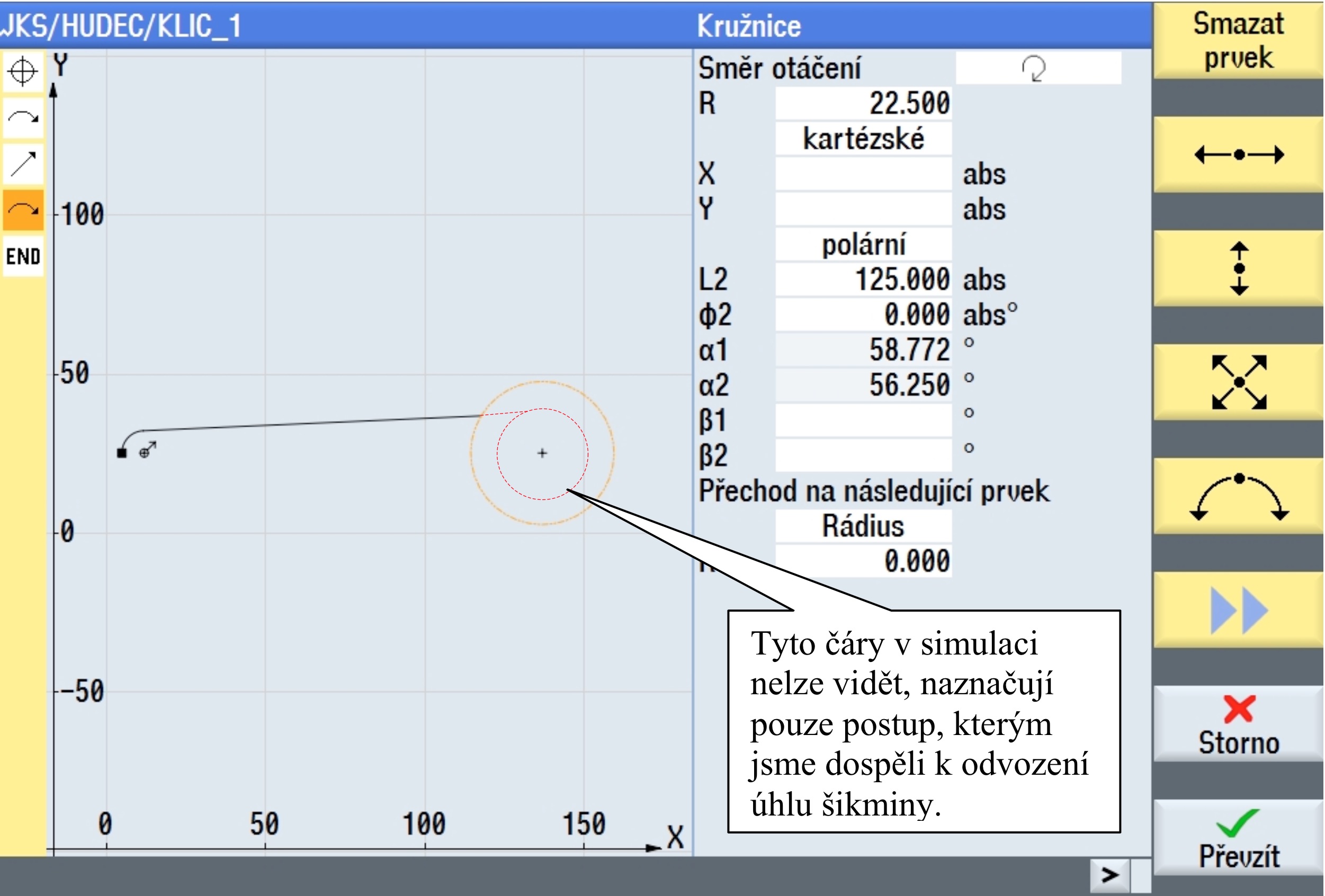
Následující tři půlkruhy již nepředstavují žádnou komplikaci. Lze je zadat kartézsky a jejich hodnoty jsou dobře zakótovány.
Obr. 297
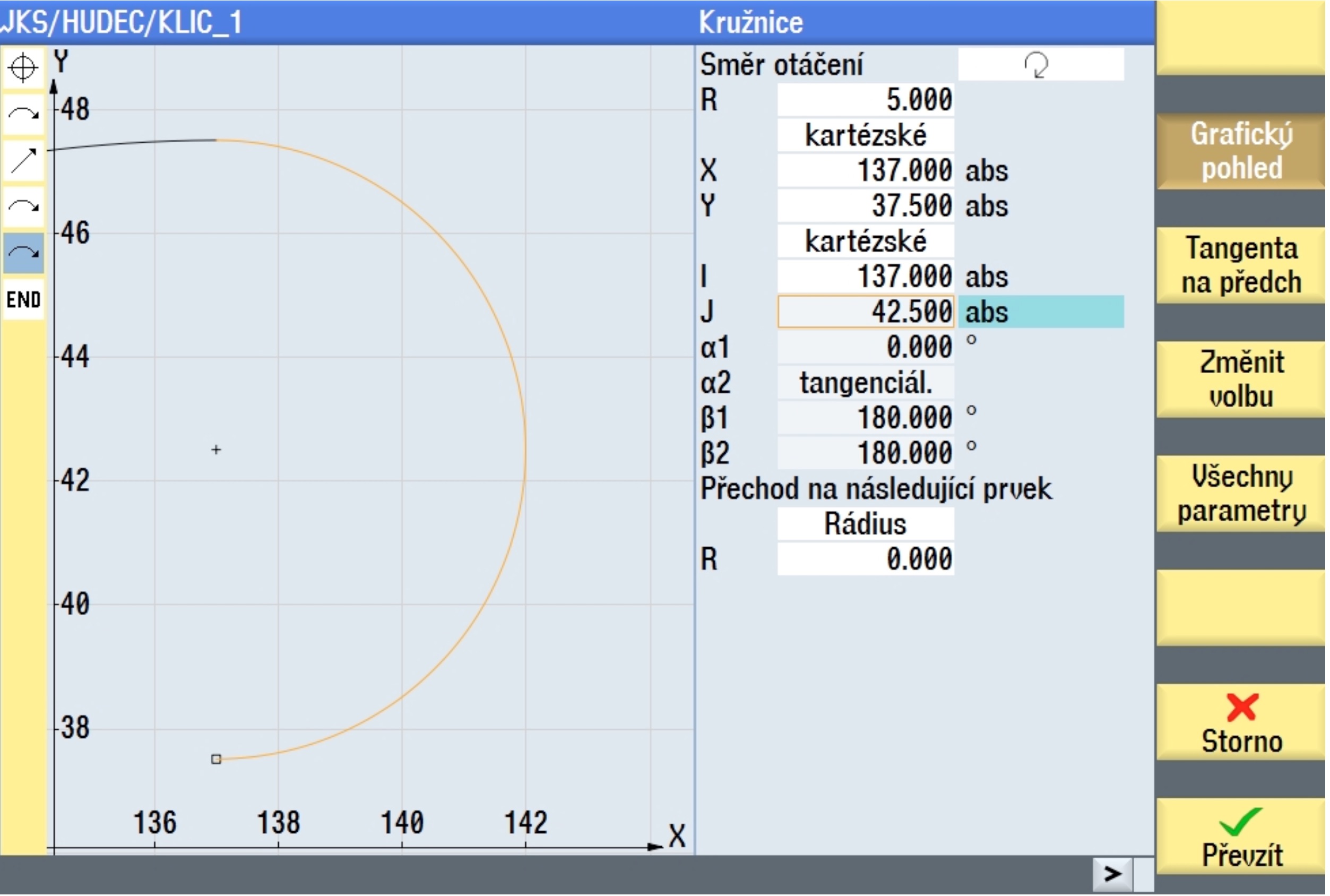
Střed oblouky R12.5 leží na horizontální ose ve stejné vzdálenosti ( X 137 ) jako středy obou menších oblouků R5. Tangenty se zobrazí automaticky, nemusíme je zadávat.
Obr. 298
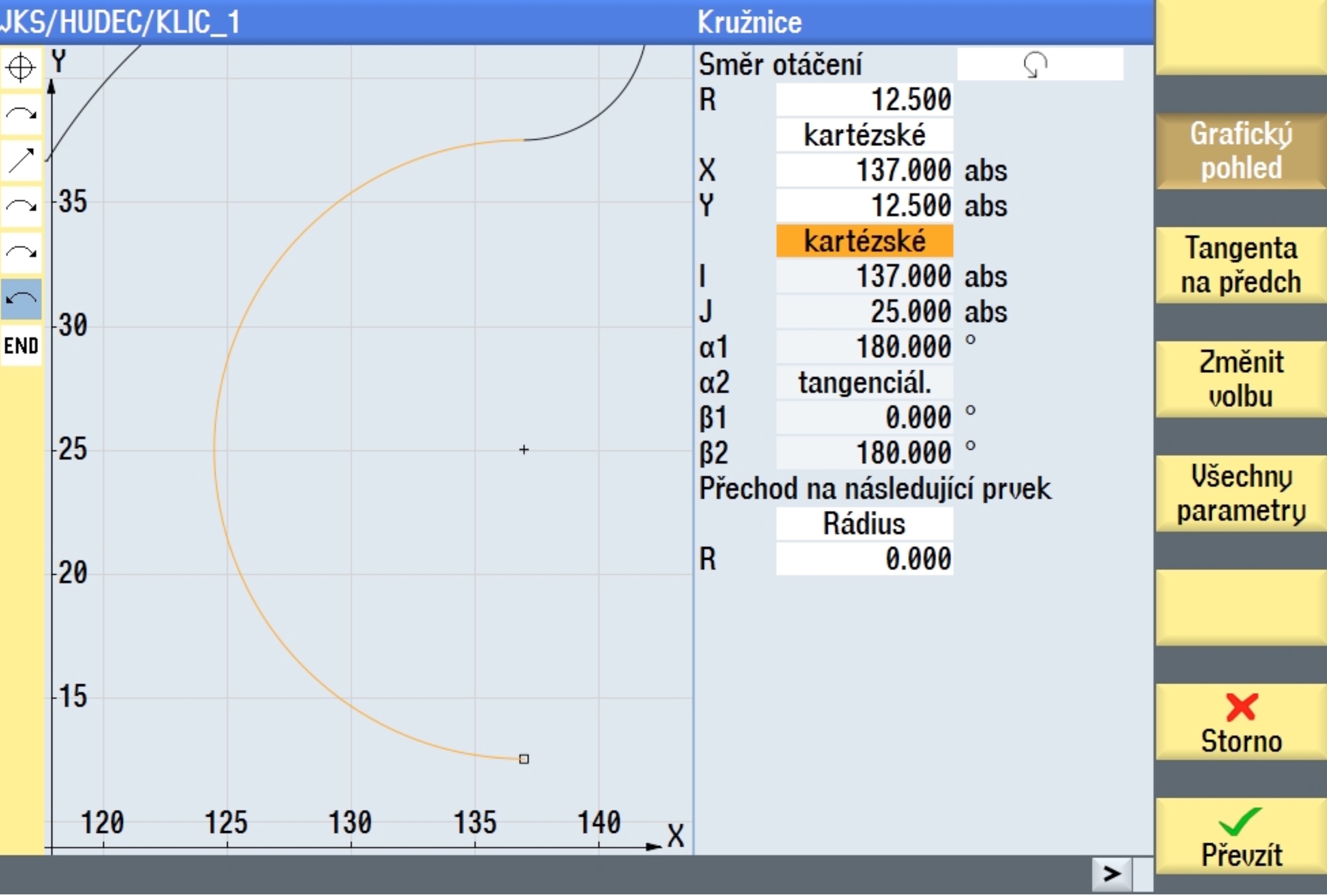
Kontura lze samozřejmě řešit mnoha způsoby. Pro zajímavost uvádím jeden z méně tradičních ale velmi pohodlných způsobu konstrukce tečného oblouku vrcholovým úhlem β2 ( 180° ).
Obr. 299
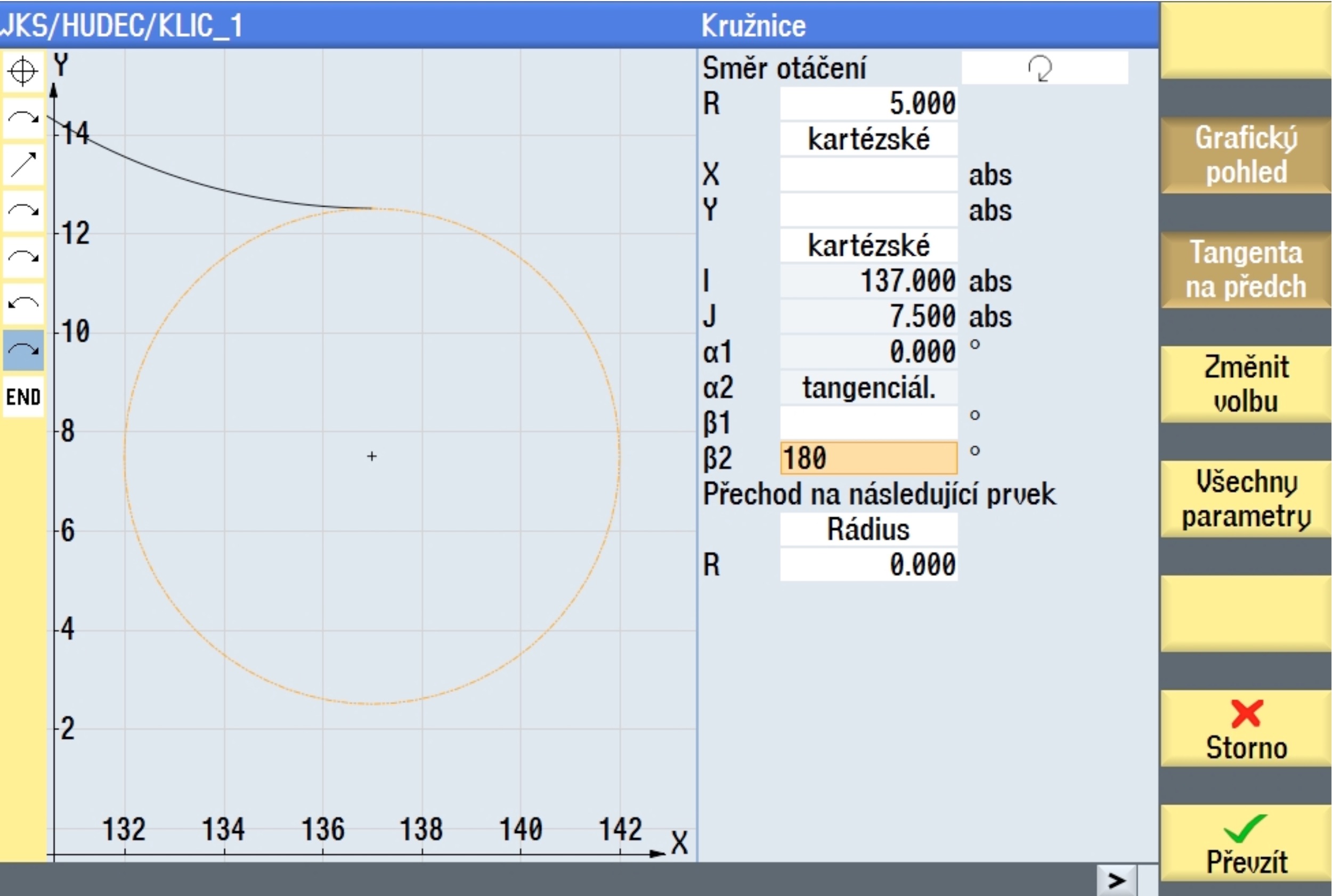
Další napojená kružnice se opět vztahuje k pólu a protože bude oříznuta šikminou ( neznáme její cílový bod ) vykreslí se nám nejprve celá. Oříznutí tedy proběhne až po napojení na následující entitu.
Obr. 300
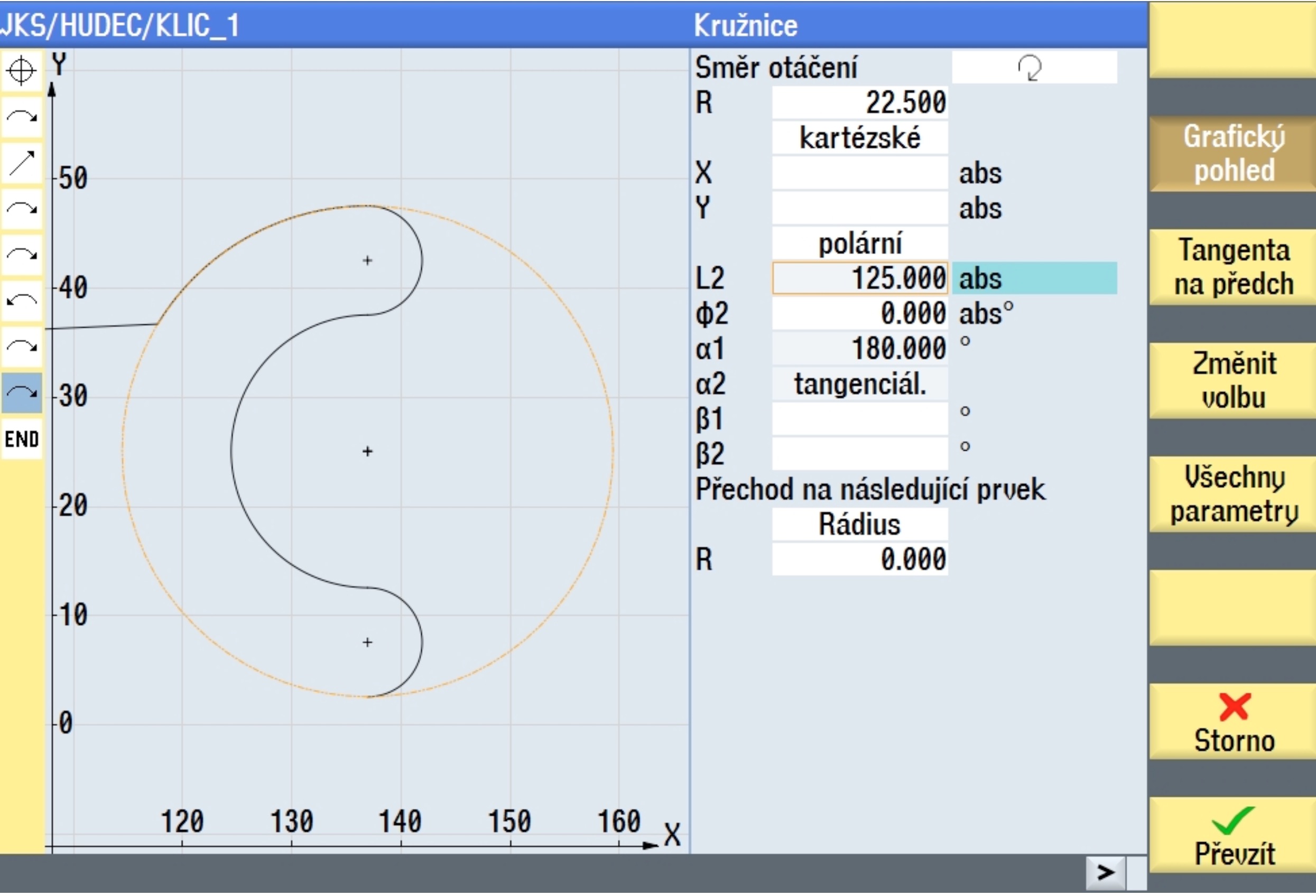
A zase je tu neznámá šikmina bez délky a úhlu. Protože je dílec osově souměrný, můžeme opět použít náš vyšetřený úhel 2.522° jen ho tentokrát ( kvůli směru entity ) přičteme k minusovému úhlu 180°. Nebo odečteme od kladného, výsledek se nezmění.
Obr. 301
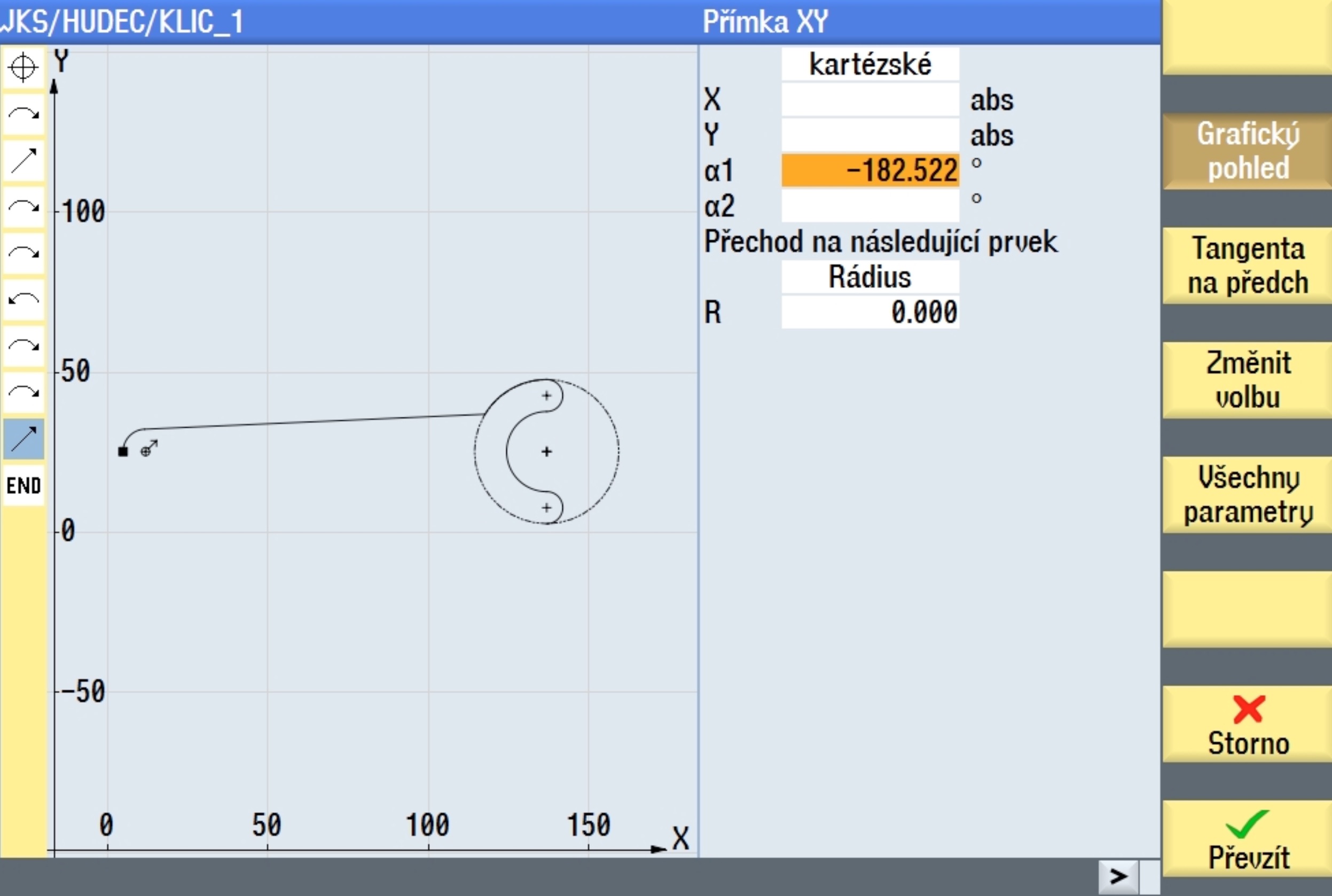
Pozor, poslední rádius, ač jeho určení zpět do startovacího bodu není těžké, nám způsobí nečekaný problém s dialogovým oknem ve kterém neuvidíme celou situaci a není tudíž jasné, co z dialogu vybrat. Bude potřeba se do entity vrátit a dialog přepnout.
Obr. 302
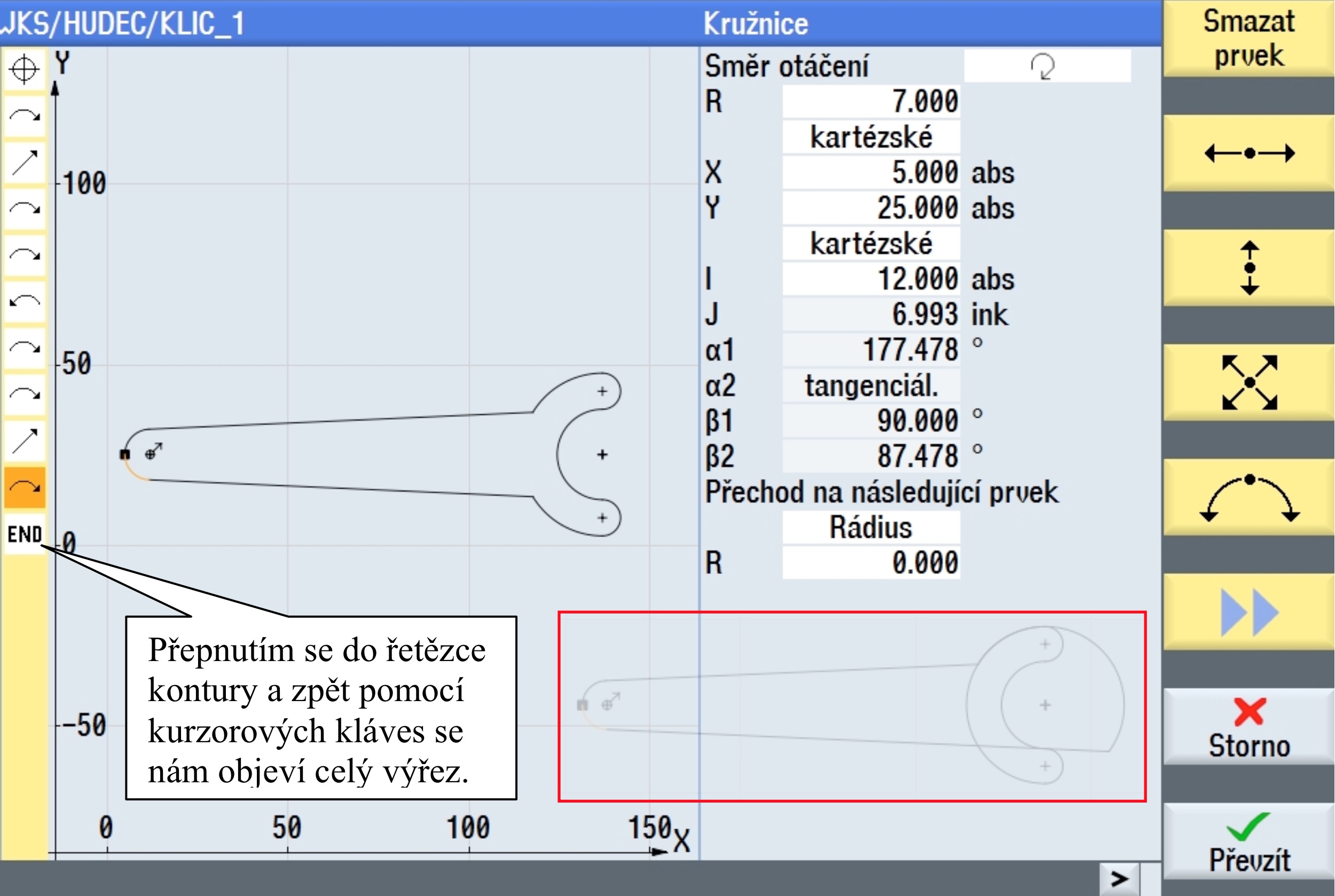
Na konec se vrátíme ve struktuře stromu jednotlivých entit a doplníme dvě zaoblení R30.
Obr. 303
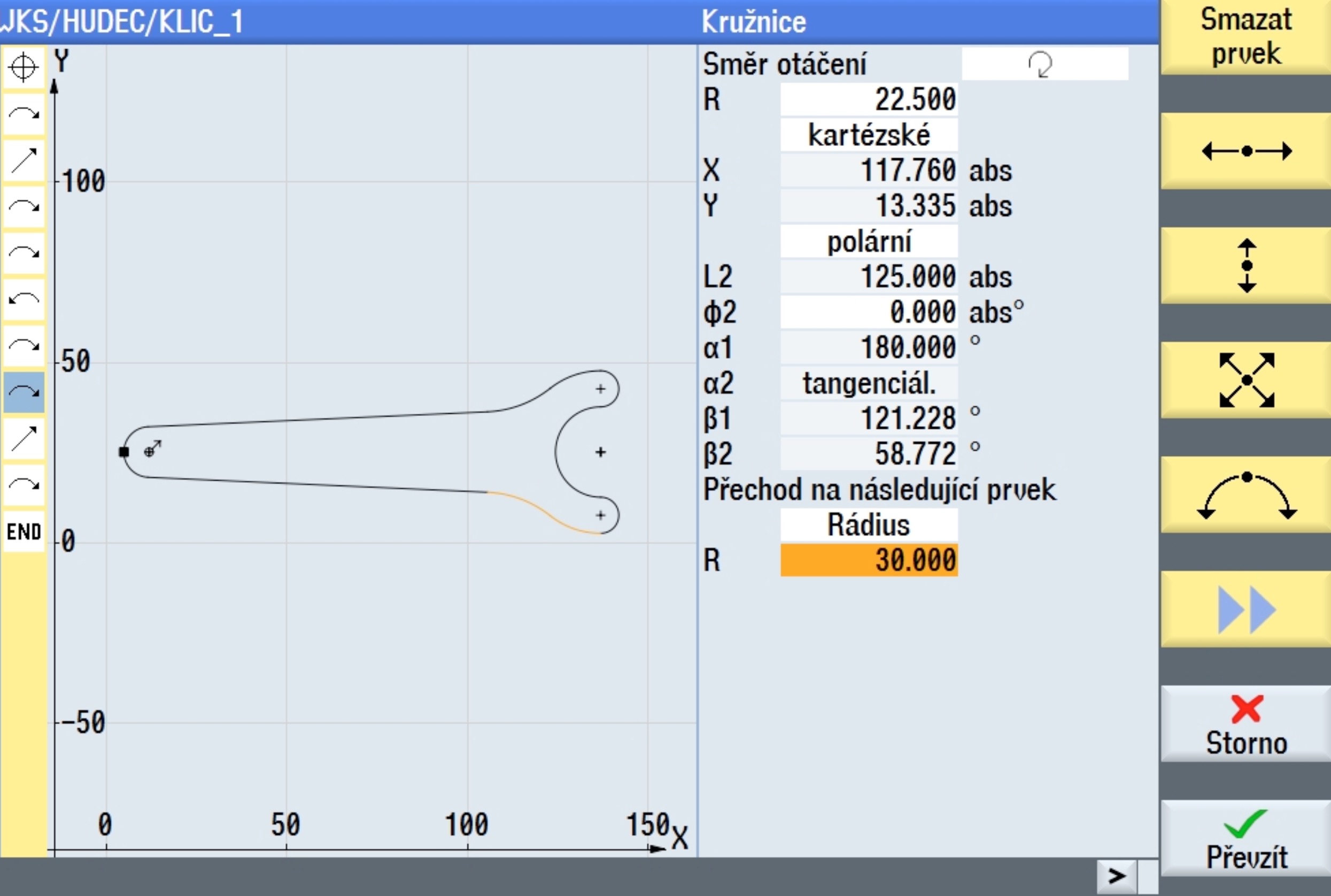
Konturu klíče můžeme opracovat, spolu s konturou polotovaru jako cyklus zámku nebo čepu. Lze ji také větším nástrojem objet po kontuře. Nezapomeňte srazit hrany čepů 0.5 x 45°.
Obr. 304
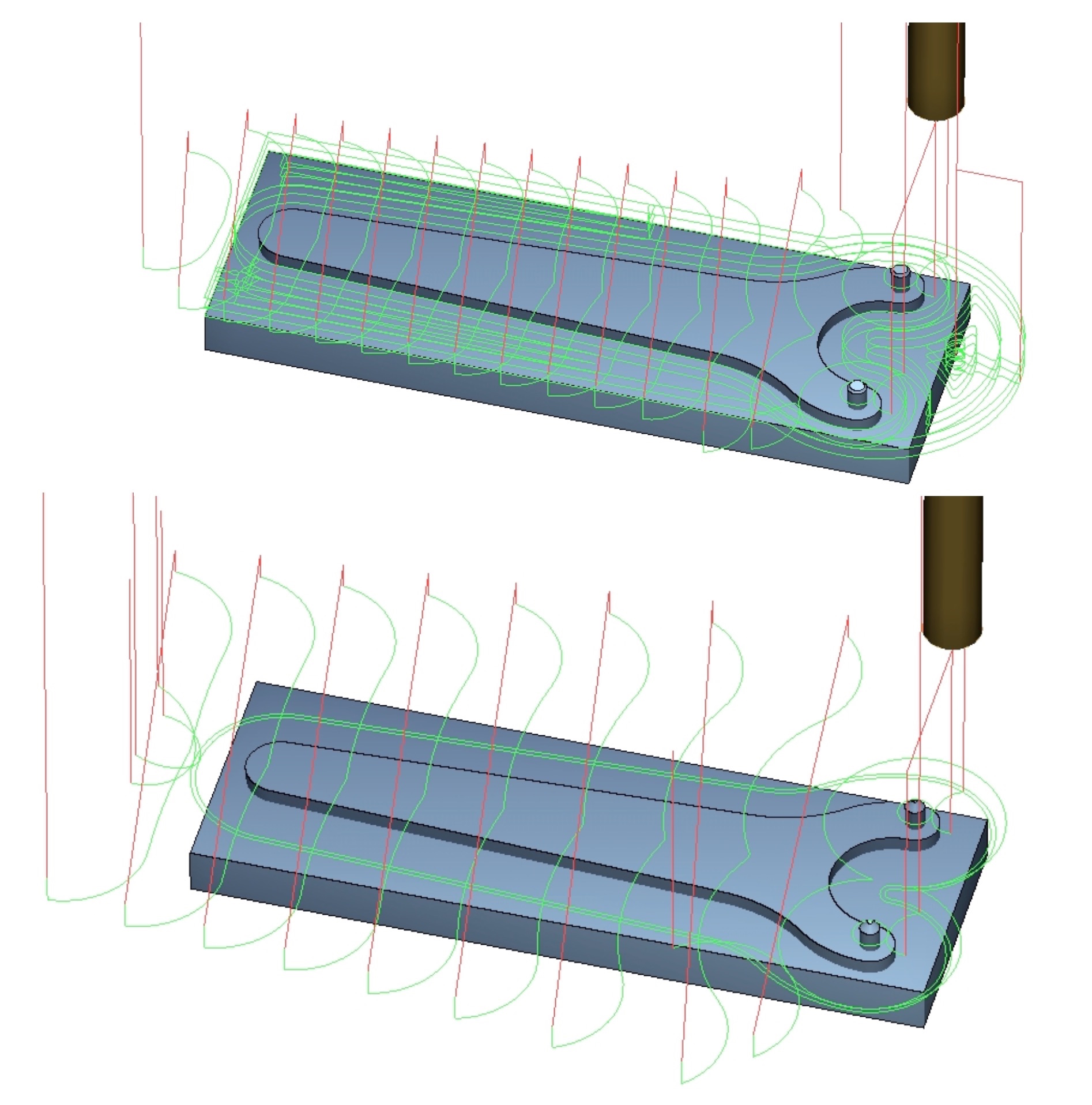
Na obrázku vidíme dráhy nástrojů při různém způsobu obrábění. Programy se liší pochopitelně i časem.